起源
牛頓法最初由艾薩克·牛頓在《流數法》( Method of Fluxions,1671年完成,在牛頓去世後的1736年公開發表)中提出。約瑟夫·鮑易也曾於1690年在 Analysis Aequationum中提出此方法。
原理
 牛頓法
牛頓法 牛頓法
牛頓法把非線性函式在處展開成泰勒級數
 牛頓法
牛頓法 藍色代表方程,紅色代表切線。
藍色代表方程,紅色代表切線。 牛頓法
牛頓法取其線性部分,作為非線性方程的近似方程, 則有
 牛頓法
牛頓法 牛頓法
牛頓法設 ,則其解為
 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法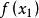 牛頓法
牛頓法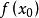 牛頓法
牛頓法 牛頓法
牛頓法因為這是利用泰勒公式的一階展開, 處並不是完全相等,而是近似相等,這裡求得的 並不能讓 ,只能說 的值比 更接近 ,於是乎,疊代求解的想法就很自然了,
 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法再把f(x)在x1 處展開為泰勒級數,取其線性部分為 的近似方程,若 ,則得 如此繼續下去,得到牛頓法的疊代公式: ,通過疊代,這個式子必然在 的時候收斂。整個過程如右圖:
 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法例1 用牛頓法求方程 在 內一個實根,取初始近似值=1.5。 解所以疊代公式為:
 搜尋方向較近似於牛頓法
搜尋方向較近似於牛頓法 牛頓法
牛頓法列表計算如下:
 牛頓法 牛頓法 | 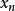 牛頓法 牛頓法 |
| 0 | 1.5 |
| 1 | 1.7371 |
| 2 | 1.6987 |
| 3 | 1.6975 |
| ... | ... |
切線法
方程f(x)=0的根就是曲線y=f(x)與x軸交點的橫坐標x*,當初始近似值x選取後,過( x,f(x))作切線,其切線方程為:y- f(x)=f′(x)(x-x)
一般地,設Xn是x*的第n次近似值,過( x,f(x))作y=f(x)的切線,其切線與x軸交點的橫坐標為: 即用切線與x軸交點的橫坐標近似代表曲線與x軸交點的橫坐標。
牛頓法正因為有此明顯的幾何意義,所以也叫切線法。
 牛頓法
牛頓法定理
設f(x)在[a,b]滿足
(1) f(a)·f(b)<0
(2) f(x)∈[a,b],f′(x),f″(x)均存在,且f′(x)與f″( x)的符號均保持不變。
(3) f(x)·f″(x)>0, x∈[a,b] 則方程f(x)=0在[a,b]上有且只有一個實根,由牛頓法疊代公式計算得到的近似解序列收斂於方程 f(x)=0 的根 x*。
由方程f(x)=0得到的牛頓疊代形式:
由於f(x*)=0,所以當f′(x*)≠0時, (x* )= 0,牛頓法至少是二階收斂的,即牛頓法在單根附近至少是二階收斂的,在重根附近是線性收斂的。
牛頓法收斂很快,而且可求復根,缺點是對重根收斂較慢,要求函式的一階導數存在。
其它例子
第一個例子
 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法求方程的根。令,兩邊求導,得。由於 ,則,即,可知方程的根位於0和1之間。我們從開始。
 牛頓法
牛頓法第二個例子
牛頓法亦可發揮與泰勒展開式,對於函式展開的功能。
求a的m次方根。
 牛頓法
牛頓法 牛頓法
牛頓法設
而a的m次方根,亦是x的解,
以牛頓法來疊代:
 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法 牛頓法
牛頓法(或)
套用
求解最值問題
牛頓法也被用於求函式的最值。由於函式取最值的點處的導數值為零,故可用牛頓法求導函式的零點,其疊代式為
 牛頓法
牛頓法
