發展歷史
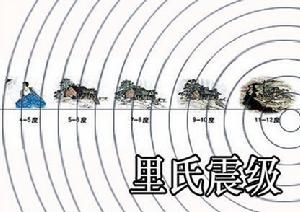 芮氏規模
芮氏規模芮氏地震規模最早是在1935年由兩位來自美國加州理工學院的地震學家裡克特(Charles Francis Richter)和古騰堡(Beno Gutenberg)共同制定的。
此標度原先僅是為了研究美國加州地區發生的地震而設計的,並用伍德·安德森扭力式地震儀(Wood-Anderson torsion seismometer)測量。里克特設計此標度的目的是區分當時加州地區發生的大量小規模地震和少量大規模地震,而靈感則來自天文學中表示天體亮度的星等。
為了使結果不為負數,里克特定義在距離震中100千米處之觀測點地震儀記錄到的最大水平位移為1微米(這也是伍德-安德森扭力式地震儀的最大精度)的地震作為0級地震。按照這個定義,如果距震中100千米處的伍德-安德森扭力式地震儀測得的地震波振幅為1毫米(103微米)的話,則震級為芮氏3級。芮氏地震規模並沒有規定上限或下限。現代精密的地震儀經常記錄到規模為負數的地震。
由於當初設計芮氏地震規模時所使用的伍德·安德森扭力式地震儀的限制,近震規模 ML 若大於約6.8或觀測點距離震中超過約600千米便不適用。後來研究人員提議了一些改進,其中面波震級(MS)和體波震級(Mb)最為常用。
震級標度
地震發生後,人們首先關心的問題是:這是多大的地震?如果回到幾百年前,我們肯定得不到像“×級地震”的類似答案,而是一系列關於地震破壞的巨觀描述,猶如明史中記載的陝西華縣地震:“……地裂泉涌,中有魚物,或城郭房陷入地中……官吏、軍民壓死八十三萬有奇”。也就是說,那個時候,我們只能根據地震的破壞程度——烈度來估計地震的大小。烈度不僅受人的主觀影響,還與震區的地質、建築條件等因素有關,因此,烈度並不能定量地度量地震大小。
1935年,查爾斯·里克特在研究美國南加州地震時,發明了一種定量測量地震大小的方法。他規定在震中距為100km的地方,如果“標準地震儀”(伍德—安德森地震儀,周期是0.8s,放大倍數為2080)記錄到的地震波最大振幅是1微米(註:儀器上記錄到1微米對應的實際地動位移是1/2080=0.00048微米),震級為0;如果振幅是x微米,震級為其對數。當然,當振幅是0.1微米時,震級為lg0.1=-1,相當於小錘子敲打地面產生的震級。實際上,絕大多數地震儀不會恰好都擺在100km震中距的地方,此時就要根據震中距對應的量規函式來校正數值。里克特提出的這種震級標度被後人稱為芮氏規模ML,也叫地方性震級,主要適用於6級以下的中小地震,這裡的L表示local(地方性)的意思。
芮氏規模的出現,第一次把地震大小變成了可測量、可相互比較的量,為地震學的定量化發展奠定了基礎。時至今日,伍德—安德森地震儀早已絕跡,成為博物館的陳列品。但人們為了保持地震記錄的對比和延續性,很多小地震仍會通過儀器的模擬仿真,計算出芮氏規模。
伍德—安德森地震儀是一種短周期地震儀(周期為0.8s),它可以較好地記錄短周期地震波。但地震波在傳播過程中,由於高頻地震波(即短周期波)的衰減速度要遠遠大於低頻地震波,當地震儀距離震中較遠時,這種地震儀的記錄能力變得有限。1945年,地震學家古登堡發明了面波震級Ms,Ms可以遠距離記錄地震,這就彌補了芮氏規模的不足。其中,s表示surface wave(面波),它是根據周期約為20s的面波大小確定的地震震級。
面波震級也存在問題,當地震的震源深度較深的時候,激發的面波不顯著。所以,古登堡還發明了體波震級mb,b表示body wave(體波),它是根據地震波的體波(通常是P波)的大小確定的地震震級。幾乎所有的地震,無論距離遠近、震源深度,還包括核爆炸,都可以在地震圖上較清楚地識別P波,因此mb具有廣泛的套用,美國地質調查局(USGS)對外公布的很多震級就是mb。
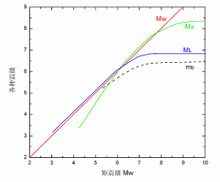
遺憾的是,無論是芮氏規模、面波震級、還是體波震級,都存在著兩個主要問題。一是這些震級與地震發生的物理過程沒有直接聯繫,物理含義不清楚。二是通過統計分析,發現它們具有“飽和”現象。也就是說,當地震所釋放的能量增大的時候,震級卻不再增大(見圖),因此面對大地震時,採用這些震級標度會低估地震的能量。
 震級
震級【矩震級(Mw)與芮氏規模(ML)、面波震級(Ms)及體波震級(mb)的關係】
1979年,日本的金森博雄提出了矩震級Mw的概念。矩震級的計算公式中用到了地震矩M0,地震矩具有嚴格的物理意義,其中M0=uAD(u是剪下模量,A是破裂面的面積,D是地震破裂的平均位錯量)。從公式看,地震破裂面面積越大,位錯量越大,釋放的能量也就越多。正因為如此,矩震級不會像其他震級一樣存在飽和問題。比如1960年智利大地震,測定的矩震級Mw=9.5,而面波震級已經飽和,僅為8.5。
矩震級已成為世界上大多數地震台網和地震觀測機構優先推薦使用的震級標度。不過,由於世界各國有各自的震級研究歷史和計算公式,各國對外公布的震級標度還未統一。中國對外公布的震級大多是面波震級而不是矩震級。比如這次日本大地震,中國公布的是面波震級8.6級,美國公布的是矩震級9.0級。
發生頻率
下表列出的是不同芮氏規模(ML)的年均發生次數和震中地區的影響:
| 程度 | 芮氏規模 | 地震影響 | 發生頻率(全球) |
| 極微 | 2.0以下 | 很小,沒感覺 | 約每天 8,000次 |
| 甚微 | 2.0-2.9 | 人一般沒感覺,設備可以記錄 | 約每天 1,000次 |
| 微小 | 3.0-3.9 | 經常有感覺,但是很少會造成損失 | 估計每年49,000次 |
| 弱 | 4.0-4.9 | 室內東西搖晃出聲,不太可能有大量損失。當地震強度超過4.5級時,已足夠讓全球的地震儀監測得到。 | 估計每年6,200次 |
| 中 | 5.0-5.9 | 可在小區域內對設計/建造不佳或偷工減料的建築物造成大量破壞,但對設計/建造優良的建築物則只會有少量的損害。 | 每年800次 |
| 強 | 6.0-6.9 | 可摧毀方圓100英里以內的居住區。 | 每年120次 |
| 甚強 | 7.0-7.9 | 可對更大的區域造成嚴重破壞。 | 每年18次 |
| 極強 | 8.0-8.9 | 可摧毀方圓數百英里的區域。 | 每年1次 |
| 超強 | 9.0及其以上 | 摧毀方圓數千英里的區域 | 每20年1次 |
震級能量
假定第1級地震所釋放的能量為1,第2級應為31.62,第3級應為1000,依此類推,第7級為10億,第8級為316.2億,第9級則為10000億。由於芮氏地震規模是常用對數,因此在估算能量的時候,芮氏規模每增加一,釋放的能量大約增加32倍。
下表列出的是不同級別的地震釋放的能量相當於的TNT當量:
| 芮氏規模 | 大致相應TNT當量 | 實例 |
| 0.5 | 6kg | 手榴彈爆炸 |
| 1.0 | 30kg | 建築爆破 |
| 1.5 | 180kg | 二戰期間常規炸彈 |
| 2.0 | 1噸 | 二戰期間常規炸彈 |
| 2.5 | 6噸 | 二戰期間的"Cookie" 巨型炸彈 |
| 3.0 | 30噸 | 2003年大型燃料空氣炸彈(MOAB) |
| 3.5 | 180噸 | 1986年前蘇聯車諾比核事故 |
| 4.0 | 1千噸 | 小型核子彈 |
| 4.5 | 0.6萬噸 | 常見的 龍捲風 |
| 5.0 | 3.3萬噸 | 美國在二戰結束前在日本 廣島 、長崎投放的核子彈(投放後日本無條件投降) |
| 5.5 | 20萬噸 | 1992年美國 內華達州 Little Skull Mtn.地震 |
| 6.0 | 100萬噸 | 1994年美國內華達州Double Spring Flat地震 |
| 6.5 | 600萬噸 | 1994年Northridge地震 |
| 7.0 | 3400萬噸 | 目前最大型的 核子彈 (註:前蘇聯曾試爆5000萬噸級別的 氫彈 ) |
| 7.5 | 1.9億噸 | 1992年美國加利福尼亞Landers地震 |
| 8.0 | 11億噸 | 1976年中國唐山大地震(7.8級)、2008年中國汶川大地震(8.0級-2008年5月18日修訂) |
| 8.5 | 62億噸 | 1964年美國阿拉斯加安克雷奇 耶穌 受難日地震 |
| 9.0 | 350億噸 | 1960年智利大地震(9.5級,為人類觀測史上最強震級)、2004年印度洋大地震(9.0級) 2011年日本大地震(9.0級)。以上三次強震均引發了巨大海嘯,造成重大人員傷亡和財產損失 |
| 10.0 | 1兆噸(1萬億噸) | 約相當於一個直徑約為100千米的石質隕石以秒速25千米撞擊地球時所產生的地震。 |
缺點及改進
芮氏地震規模的主要缺陷在於它與震源的物理特性沒有直接的聯繫,並且由於“地震強度頻譜的比例定律”(The Scaling Law of Earthquake Spectra)的限制,在8.3-8.5左右會產生飽和效應,使得一些強度明顯不同的地震在用傳統方法計算後得出芮氏地震規模(如(MS)數值卻一樣。到了21世紀初,地震學者普遍認為這些傳統的地震規模表示方法已經過時,轉而採用一種物理含義更為豐富,更能直接反應地震過程物理實質的表示方法即矩震級 (Moment magnitude scale,MW)。地震矩規模是由同屬加州理工學院的金森博雄(Hiroo Kanamori)教授於1977年提出的。該標度能更好的描述地震的物理特性,如地層錯動的大小和地震的能量等。