引發原因
系統的初始狀態為零,僅由激勵源引起的回響被稱之為該系統的“零狀態回響”。
實例:一個原來沒有充過電的電容器通過電阻與電源接通,構成充電迴路,那么電容器兩端的電壓或迴路中的電流就是系統零狀態回響。
本質
系統的零狀態回響一般分為兩部分,它的變化形式分別由系統本身的特性和激勵源所決定。當系統是線性的,它的特性可以用線性微分方程表示時,零狀態回響的形式是若干個指數函式之和再加上與激勵源形式相同的項。前者是對應的齊次微分方程的解,其中指數函式的個數等於微分方程的階數,也就是系統內部所含“獨立”儲能元件的個數。後者是非齊次方程的特解。對於實際存在的無源系統而言,零狀態回響中的第一部分將隨著時間的推移而逐漸地衰減為零,因此往往又把這一部分稱之為回響的“暫態分量”或“自由分量”;後者與激勵源形式相同的部分則被稱之為“穩態分量”或“強制分量”。
全回響
系統的全回響是系統或電路在輸入和初始條件共同作用下的回響。其可以分成零輸入回響和零狀態回響兩種分量,也可以分成自然回響和受迫回響兩種分量,還可以分成瞬態回響和穩態回響兩種分量。
求解方法
連續線性時不變系統零狀態回響的分析方法 :
時域分析
1. 時域經典分析法:指利用數學經典理淪,來求解系統微分方程的過程
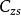 零狀態回響
零狀態回響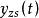 零狀態回響
零狀態回響步驟:(1)構建系統的時域微分方程;(2)列寫特徵多項式,求出特徵根;(3)求解出方程的齊次解、特解的一般形式;(4)將全解表達式帶回原方程,得出待定係數 ,求出 表達式
說明:微分方程的全解由齊次解和特解兩部分組成,其中齊次解的形式由微分方程對應的齊次方程的特徵根確定,特解由輸入激勵的形式決定。
時域經典解析法具有下面特點:
(1)優點:思路清晰,便於理解
(2)缺點:用到數學知識,運算量較大,對於複雜輸入信號,不易求得特解。
2. 時域卷積法
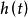 零狀態回響
零狀態回響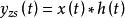 零狀態回響
零狀態回響步驟:(1)構建系統的時域微分方程;(2)求出衝激回響 ;(3)計算零狀態回響
時域卷積法具有下面特點:
(1)優點:適用於複雜輸入信號時的零狀態回響的分析。
(2)缺點:要計算系統的衝激回響及卷積積分,過程繁瑣。
頻域(復頻域)分析
1. 頻域分析法
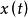 零狀態回響
零狀態回響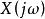 零狀態回響
零狀態回響步驟:(1)構建系統的頻域電路代數方程;(2)解代數方程,求取系統的頻率回響;(3)根據傅立葉變換公式,計算輸入信號 的傅立葉變換式 ;(4)根據傅立葉變換的時域卷積性質有:
綜上分析過程,頻域分析法特點:
(1)優點:將時域卷積積分轉換到頻域乘積,或將時域微分方程轉換為頻域代數方程,簡化計算。並引入了頻譜函式的概念,對求解衝激回響很有幫助。
(2)缺點:不滿足絕對可積條件的信號,其傅立葉變換無意義或不存在。
2. 復頻域分析法
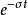 零狀態回響
零狀態回響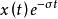 零狀態回響
零狀態回響為了解決頻域分析中的局限性這一問題,將任意連續信號乘上一個衰減因子使得兩者的乘積絕對可積,然後再對進行傅立葉變換。這樣傅立葉變換就轉換為拉普拉斯變換。
步驟:
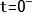 零狀態回響
零狀態回響方法1:(1)構建系統的復頻域代數方程,令輸出量及其各階導數在時的值為零。(2)對輸出量的復頻域函式取逆變換,既得系統的零狀態回響。
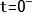 零狀態回響
零狀態回響方法2:(1)構建系統的復頻域代數方程,並令輸出量及其各階導數在時的值為零。(2)求出系統函式
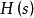 零狀態回響
零狀態回響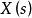 零狀態回響
零狀態回響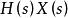 零狀態回響
零狀態回響,輸入信號的拉氏變換。(3)利用拉氏變換卷積性質,求的積的拉氏逆變換,既得零狀態回響。
復頻域分析法的特點:
將時域卷積積分轉換到復頻域乘積,或將時域微分方程計算轉換到復頻域代數方程,簡化計算,而且也解決了頻域分析的局限性問題。

