基本概念
單位階躍函式
單位階躍函式（Unit Step Function）屬於典型輸入信號，其定義為 ：
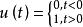單位階躍回響
單位階躍回響很明顯的一點是，單位階躍函式在t=0這一點是不連續的。
單位階躍回響
單位階躍回響，就是指系統在接收到單位階躍函式輸入後產生的零狀態回響。
所謂零狀態回響是指系統在接收到指定輸入之前處於初始狀態，即保證系統是完全因為指定輸入（在此為單位階躍輸入）而產生的回響變化。
單位脈衝回響
單位脈衝回響是指系統對單位脈衝輸入的回響。單位脈衝信號是一個無窮大的瞬時衝激，表示為：
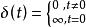單位階躍回響單位脈衝信號在時間上的積分是1。
對於 n 階線性定常系統，由線性性和疊加原理，在零初值條件下，系統的單位階躍回響函式的導數為該系統的單位脈衝回響函式。
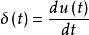單位階躍回響作用與意義
系統動態性能分析
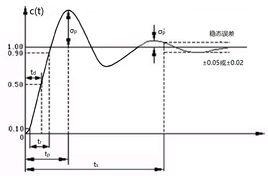
動態性能是系統性能的一個十分重要的指標，通常用階躍信號作用來測定系統的動態性能。
一般認為，階躍信號對於系統來說是十分嚴峻的工作狀態，因為階躍信號中存在躍斷點（不連續點）。
針對零初始狀態系統在單位階躍輸入下的回響情況，定義了一系列動態性能指標，用以評判系統的動態性能，如超調量、衰減比、上升時間、調節時間、峰值時間等等。
建立系統回響模型
對於典型的輸入信號，如衝激信號、階躍信號、斜坡信號等，都建立有回響模型（在此即單位階躍回響模型）。根據模型，可以快速判斷出實際系統的動態性能指標參數，只需要代入實際系統的相關測量參數，就可以 定量分析其性能指標。
數學模型
一階系統的單位階躍回響
設單位階躍信號r(t)=1(t)，其拉氏變換為R(t)=1/s。
一階系統的傳遞函式為：
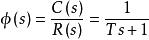單位階躍回響代入R(s)得到：
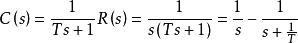單位階躍回響反拉氏變換：
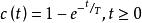單位階躍回響
單位階躍回響如圖所示，設定時間常數T=1得到該圖。
按照動態性能定義，調節時間等於3T（△=5%）或4T（△=2%）。
欠阻尼二階系統的單位階躍回響
二階系統的傳遞函式為：
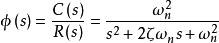單位階躍回響代入R(s)得到：
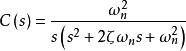單位階躍回響反拉氏變換：
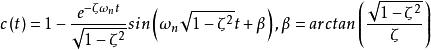單位階躍回響
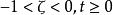單位階躍回響
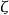單位階躍回響
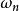單位階躍回響其中 為阻尼比（相對阻尼係數）， 為自然頻率（無阻尼振盪頻率）。
二階系統相比一階系統要複雜的多，根據阻尼比和自然頻率可以對系統進行分析。
一般根據阻尼比的值，分為欠阻尼、臨界阻尼、過阻尼三種情況（另外也有無阻尼情況）。
高階系統的回響情況更為複雜，一般藉助計算機進行分析計算。
函式推導
假設已知一個n階線性定常系統的單位階躍回響為c(t)，則其傳遞函式推導如下：
1. 首先根據c(t)得到系統的階次，假設為n階系統；
2. 判斷c(0)、c'(0)、... 是否為0，假設c(t)在t=0處的m階導不為0（m<n）；
3. 則可以構造傳遞函式為
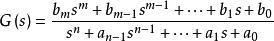單位階躍回響
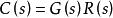單位階躍回響4. 由可以得到系統微分方程，將c(t)以及其在t=0處的各階導數可以得到G(s)中的係數。
