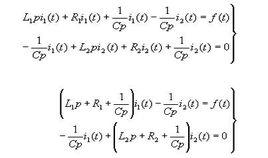定義:
但值得注意的是,雖然自由回響的形式是由系統自身決定的,與激勵無關;但這並不意味著自由回響和激勵無關,事實上自由回響和激勵是相關的。
自由回響不等同於零輸入回響,自由回響=零輸入回響+零狀態回響中的一部分。
相關:
強迫回響
動態電路微分方程的特解形式,僅僅由激勵決定,稱為強迫回響;
暫態回響
動態電路全回響中,當t→∞時,趨於0的部分,稱為暫態回響;
穩態回響
動態電路全回響中,除去暫態回響,剩下的部分稱為穩態回響。
全回響
全回響=自由回響+強迫回響,等號右端第一項的變化規律與外加激勵的變化規律無關,稱為自由回響 分量;等號右端第二項的變化規律與外加激勵的變化規律相同,稱為強迫回響分量。即全回響可分解為自由回響與強迫回響之和。
同時全回響也可以分解為暫態回響和穩態回響,即全回響=暫態回響+穩態回響。
全回響還可以分解為零輸入回響和零狀態回響,既全回響還=零輸入回響+零狀態回響。
它們僅僅是從不同的角度進行分類。
求解方法:
時域求解
一般給有系統的微分方程(時域微分方程),通過列出特徵方程(令e(t)=0),求得方程的齊次解,即為系統的自由回響。這裡求得的自由回響僅僅是種形式,因為它含有未知參數。通過代入初始條件(即回響的N階導數在t=0+時的值),解得未知參數。這時得出的結果就是回響的完整的自由分量。
S域求解
首先要有激勵的S域形式表達式E(s)(註:可以通過其他方法求得這個表達式),再把電路圖轉換到S域,很容易寫出傳遞函式H(s)。又有R(s)=H(s)E(s),這樣就得到了S域的全回響。把S域全回響轉換回時間域r(t)在r(t)中找出與系統固有頻率一致的那幾項,即為自由回響(確切地說是自由分量)。