常見激勵函式
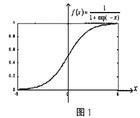
Sigmoid函式。是連續,可導,有界,關於原點對稱的增函式,呈S形,具體可用反正切函式arctan或指數函式exp來實現,如f(x)=arctan(x)/(pi/2), f(x)=1/(1+e-x);
階躍函式;是sigmoid函式的不可導版本;
 激勵函式
激勵函式徑向基函式。是函式值沿從輸入空間中某點向外輻射的徑向射線變化的函式。在空間呈球形。
定義
神經網路中的每個節點接受輸入值,並將輸入值傳遞給下一層。輸入節點會將輸入屬性值直接傳遞給下一層(隱層或輸出層)。在神經網路中,隱層和輸出層節點的輸入和輸出之間具有函式關係,這個函式稱為激勵函式(Activation Function)。
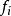 激勵函式
激勵函式神經網路中每個結點i的輸出都基於相關的激勵函式的定義。激勵函式有時也叫處理單元函式或壓縮函式。它用於輸入弧上的一組輸入。激勵函式也叫點火規則,這使它與人腦的工作聯繫起來。當一個神經元的輸入足夠大時,就會點火,也就是從它的軸突(輸出連線)傳送電信號。同樣,在人工神經網路中,只要輸入超過一定標準時才會產生輸出,這就是點火規則的思想。當只處理二值輸出時,輸出要么為0要么為1,取決於神經元是否應該點火。
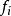 激勵函式
激勵函式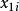 激勵函式
激勵函式 激勵函式
激勵函式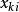 激勵函式
激勵函式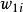 激勵函式
激勵函式 激勵函式
激勵函式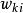 激勵函式
激勵函式激勵函式套用於一組輸入值{,,}和權值{,,},這些輸入值通常以乘積之和的形式
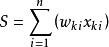 激勵函式
激勵函式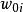 激勵函式
激勵函式合併到一起。如果存在偏移,則公式需加上。
兩個條件
多種函式可以作為激勵函式,只需要滿足兩個條件:
1.函式必須輸出 [0,1]之間的值;
2.函式在充分活躍時,將輸出一個接近1的值,表示從未在網路中傳播活躍性。
類型
函式
線性激勵函式基於輸入產生一個線性輸出值。
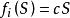 激勵函式
激勵函式,其中c是一個正的常數。這是一個常見的線性激勵函式。
對於線性函式,輸出沒有最大值和最小值方面的限制。
閾值
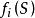 激勵函式
激勵函式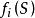 激勵函式
激勵函式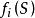 激勵函式
激勵函式階躍激勵函式的輸出值為1或0,它取決於輸入值和相應權值的乘積之和,當乘積之和高於閾值T時,所對應的的值為1,否則為0。輸出值也可以是-1或1。另外,1還可以被任何常數所替代。這種“硬性限制”閾值函式的一個變種是線性閾值函式。線性閾值函式也叫作斜坡函式或分段線性函式,這種激勵函式的值從小到大逐漸增加。下面的函式就是一個線性閾值函式,滿足:
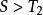 激勵函式
激勵函式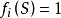 激勵函式
激勵函式(1)當時,;
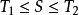 激勵函式
激勵函式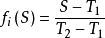 激勵函式
激勵函式(2)當時,;
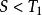 激勵函式
激勵函式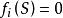 激勵函式
激勵函式(3)當時,;
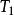 激勵函式
激勵函式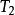 激勵函式
激勵函式這裡的線性增長存在於和之間。與一般的閾值函式類似,這裡函式的取值可以在-1~1之間,也可以在0~1之間。
S形
S形激勵函式是一個輸出值在-1~1之間(或0~1之間)的S形曲線,它是單調增加的。雖然S形函式有幾種類型,但是它們都具有“S”形特徵。
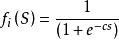 激勵函式
激勵函式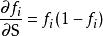 激勵函式
激勵函式一個常見的S形函式是logistic函式:,其中c是一個正的常數,它可以改變函式的傾斜程度。該函式的導數很簡單:。
雙曲正切
S形函式的一個變種是雙曲正切函式,如:
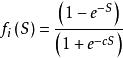 激勵函式
激勵函式該函式有一個以0為中心的輸出。
高斯
高斯函式是一個輸出值在區間 [0,1]上的鐘形曲線。
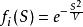 激勵函式
激勵函式一個典型的高斯函式是:,其中S是均值,V是預先定義的表示方差的正值。
逆函式積分和
求取激勵函式逆函式積分和的目的是為了配合所設計的能量函式的數值計算,但是該值得求取具有以下困難:
(1)逆函式無法用數學解析表達;
(2)要對逆函式積分並不容易;
(3)即使可以積分,也會很浪費時間,不適宜在算法疊代中直接使用。
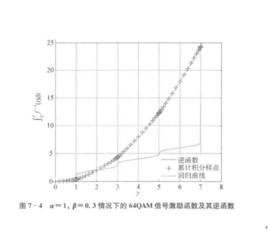
為了解決上述問題,這裡將以64QAM信號的激勵函式為例來闡述求取改該值的方法:
(1)利用正函式,求關於逆函式的積分;
(2)利用Cumtrapz求在區間段的積分採樣值;
(3)利用多項式進行最小二乘回歸,獲得回歸函式的回歸擬合曲線。
只要預先獲得激勵函式的逆函式積分和,就可以很容易地構造出對應的搜尋表,然後在疊代中直接採用查表方法獲得相應的值,或者可以根據擬合回歸函式進行近似計算逆函式積分和的值。