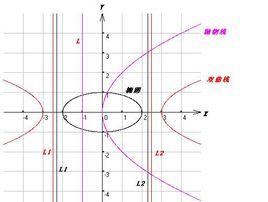
圓錐曲線的準線方程
橢圓
準線:垂直於長軸所在直線的直線
橢圓: (x^2/a^2)+(y^2/b^2)=1(a>b>0)
準線方程為:x=±a^2/c
雙曲線
雙曲線:(x^2/a^2)-(y^2/b^2)=1
準線方程為:x=±a^2/c
拋物線
1、拋物線:y^2=2px
準線方程為:x=-p/2
2、拋物線:y^2=-2px
準線方程為:x=p/2
幾何性質
準線到頂點的距離為Rn/e,準線到焦點的距離為P = Rn(1+e)/e = L0/e 。
當離心率e大於零時,則P為有限量,準線到焦點的距離為P = Rn(1+e)/e = L0/e 。
當離心率e等於零時,則P為無限大,P是非普適量。用無限遠來定義圓錐曲線是不符合常理的。
教科書中定義局限性的原因是不了解準線的幾何性質,當e等於零時則準線為無限遠,準線是非普適量,是局限性的量。教科書中用準線來定義圓錐曲線不包含圓的原因。
錐面上的準線
定義
在空間曲面一般理論中,曲面可以看作一族曲線沿其準線運動所形成的軌跡,對曲線族生成曲面而言,準線就是和曲線族中的每一條曲線均相交的空間曲線.。準線方程的確定對於研究曲面的幾何特徵和形狀有著重要的價值。 一方面,確定一條準線的方程是建立曲面方程的前提,另一方面對於給定方程的曲面的幾何特徵也可通過其上的一條準線方程研究。
定義1,對於空間中的一條曲線 Γ 和不在曲線Γ 上的一點A,通過點A並與曲線Γ 相交的一族直線構成的曲面稱為錐面,這些直線都稱為錐面的母線,曲線Γ 稱為錐面的準線。
引理1,一個關於x-a,y-b,z-c的n(n>0)次齊次方程表示一個以A(a,b,c)為頂點的錐面。
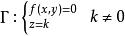 準線
準線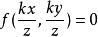 準線
準線引理2,以 為準線,頂點在原點的錐面方程為 。
引理3,錐面與過錐面頂點的平面的交線或者為頂點或者為直線。
一般錐面準線方程的特徵
由定義1可知,空間中任意一條不過頂點且與錐面每一條直母線相交的曲線均可作為錐面的準線,於是特別地,取一個不過頂點,且與每條直母線均相交的平面,其與錐面的交線可作為錐面的準線.下面的定理結合準線的幾何特徵,給出一種準線的解析式。
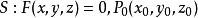 準線
準線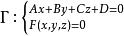 準線
準線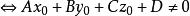 準線
準線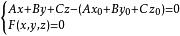 準線
準線定理2,設錐面 為S的頂點,則 為S的一條準線 ,且 不表示直線(或者說只表示一個點)。
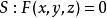 準線
準線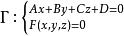 準線
準線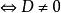 準線
準線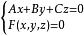 準線
準線推論1,設 為頂點在原點的錐面,則 為S的一條準線 ,且方程組 只有零解。