漸近線特點
無限接近,但不可以相交。分為垂直漸近線、水平漸近線和斜漸近線。
當曲線上一點 M沿曲線無限遠離原點時,如果 M到一條直線的距離無限趨近於零,那么這條直線稱為這條曲線的 漸近線。
需要注意的是:並不是所有的曲線都有漸近線,漸近線反映了某些曲線在無限延伸時的變化情況。
根據漸近線的位置,可將漸近線分為三類:水平漸近線、垂直漸近線、斜漸近線。
y=k/x(k≠0)是反比例函式,其圖象關於原點對稱,x=0,y=0為其漸近線方程
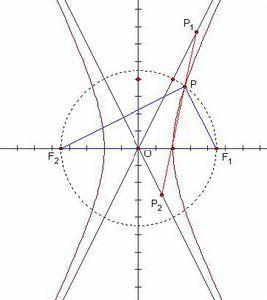
當焦點在x軸上時 雙曲線漸近線的方程是y=[±b/a]x
當焦點在y軸上時 雙曲線漸近線的方程是y=[±a/b]x
幾何性質
1.雙曲線 x^2/a^2-y^2/b^2 =1的簡單幾何性質
(1)範圍:|x|≥a,y∈R.
(2)對稱性:雙曲線的對稱性與橢圓完全相同,關於x軸、y軸及原點中心對稱.
(3)頂點:兩個頂點A1(-a,0),A2(a,0),兩頂點間的線段為實軸,長為2a,虛軸長為2b,且c^2=a^2+b^2.與橢圓不同.
(4) 漸近線:雙曲線特有的性質
方程:y=±(b/a)x(當焦點在x軸上),y=±(a/b)x (焦點在y軸上)
或
令雙曲線標準方程 x^2/a^2-y^2/b^2 =1中的1為零即得漸近線方程.
(5)離心率e>1,隨著e的增大,雙曲線張口逐漸變得開闊.
(6)等軸雙曲線(等邊雙曲線):x2-y2=a2(a≠0),它的漸近線方程為y=±b/a*x,離心率e=c/a=√2 (7)共軛雙曲線:方程 x^2/a^2-y^2/b^2=1與x^2/a^2-y^2/b^2=-1 表示的雙曲線共軛,有共同的漸近線和相等的焦距,但需注重方程的表達形式.
注意
1.與雙曲線 - =1共漸近線的雙曲線系方程可表示為 - =λ(λ≠0且λ為待定常數)
2.與橢圓 =1(a>b>0)共焦點的曲線系方程可表示為 - =1(λ0時為橢圓, b2<λ<a2時為雙曲線)
2.雙曲線的第二定義
平面內到定點F(c,0)的距離和到定直線l:x=+(-)aˆ2/c 的距離之比等於常數e=c/a (c>a>0)的點的軌跡是雙曲線,定點是雙曲線的焦點,定直線是雙曲線的準線,焦準距(焦參數)p= a2/c,與橢圓相同.
3.焦半徑( - =1,F1(-c,0)、F2(c,0)),點p(x0,y0)在雙曲線 - =1的右支上時,|pF1|=ex0+a,|pF2|=ex0-a;
P在左支上時,則 |PF1|=ex1+a |PF2|=ex1-a.