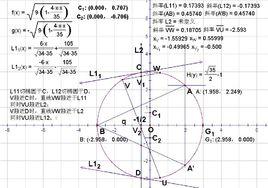
準線的定義
準線方程 x=a^2/c (X的正半軸) x=-a^2/c(X的負半軸)
橢圓
橢圓上P點坐標(x0,y0)0<c/a=(xo+p/2) /丨PF丨<1
當動點P到定點F(焦點)和到定直線X=Xo的距離之比為離心率時,該直線便是橢圓的準線。
準線方程 x=a^2/c x=-a^2/c
雙曲線
雙曲線上P點坐標(x0,y0)c/a=(xo+p/2) /丨PF丨>1
對於雙曲線方程(以焦點在X軸為例)( x^2/a^2-y^2/b^2=1 (a,b>0)亦可定義成:當動點P到定點O和到定直線X=Xo的距離之比為離心率時,該直線便是雙曲線的準線。)
準線方程 x=a^2/c x=-a^2/c
拋物線
拋物線(以開口向右為例) y^2=2px(p>0)(亦可定義成:當動點P到焦點F和到定直線X=Xo的距離之比恆等於1時,該直線是拋物線的準線。)
準線方程: x=-p/2
設拋物線上P點坐標(x0,y0)c/a=(xo+p/2) /丨PF丨=1
(ps:x^2=2py(p>0)時。準線方程為y=-p/2)
準線的性質
圓錐曲線上任意一點到一焦點的距離與其對應的準線(同在Y軸一側的焦點與準線)對應的距離比為離心率。
橢圓上任意一點到焦點距離與該點到相應準線距離的比等於離心率e.