定義
金融數學(FinancialMathematics),又稱數理金融學、數學金融學、分析金融學,是利用數學工具研究金融,進行數學建模、理論分析、數值計算等定量分析,以求找到金融學內在規律並用以指導實踐。金融數學也可以理解為現代數學與計算技術在金融領域的套用,因此,金融數學是一門新興的交叉學科,發展很快,是目前十分活躍的前言學科之一。
21世紀數學技術和計算機技術一樣成為任何一門科學發展過程中的必備工具。美國花銀行副總裁柯林斯(Collins)1995年3月6日在英國劍橋大學牛頓數學科學研究所的講演中敘述到:“在18世紀初,和牛頓同時代的著名數學家伯努利曾宣稱:‘從事物理學研究而不懂數學的人實際上處理的是意義不大的東西。’那時候,這樣的說法對物理學而言是正確的,但對於銀行業而言不一定對。在18世紀,你可以沒有任何數學訓練而很好地運作銀行。過去對物理學而言是正確的說法現在對於銀行業也正確了。於是現在可以這樣說:‘從事銀行業工作而不懂數學的人實際上處理的是意義不大的東西’。”他還指出:花旗銀行70%的業務依賴於數學,他還特彆強調,‘如果沒有數學發展起來的工具和技術,許多事情我們是一點辦法也沒有的……沒有數學我們不可能生存。”這裡銀行家用他的經驗描述了數學的重要性。在冷戰結束後,美國原先在軍事系統工作的數以千計的科學家進入了華爾街,大規模的基金管理公司紛紛開始僱傭數學博士或物理學博士。這是一個重要信號:金融市場不是戰場,卻遠勝於戰場。但是市場和戰場都離不開複雜艱深,迅速的計算工作。
現狀及發展
 金融市場
金融市場在國內不能迴避這樣一個事實:受過高等教育的專業人士都可以讀懂國內經濟類,金融類核心期刊,但國內金融學專業的本科生卻很難讀懂本專業的國際核心期刊《Journal of Finance》,證券投資基金經理少有人去閱讀《Joural of Portfolio Management》,其原因不在於外語的熟練程度,而在於內容和研究方法上的差異,國內較多停留在以描述性分析為主著重描述金融的定義,市場的劃分及金融組織等,或稱為描述金融;而國外學術界以及實務界則以數量性分析為主,比如資本資產定價原理,衍生資產的複製方法等,或稱為分析金融,即使在國內金融學的教材中,雖然涉及到了標的資產(Underlying asset)和衍生資產(Derivative asset)定價,但對公式提出的原文證明也予以迴避,這種現象是不合理的,產生這種現象的原因有如下幾個方面:首先,根據研究方法的不同,我國金融學科既可以歸到我國哲學社會科學規劃辦公室,也可以歸到國家自然科學基金委員會管理科學部,前者占主要地位,且這支隊伍大多來自經濟轉軌前的哲學和政治學隊伍,因此研究方法多為定性的方法。而西方正好相反,金融研究方向的隊伍具有很好的數理功底。其次是我國的金融市場的實際環境所決定。我國證券市場剛起步,也沒有一個統一的貨幣市場,投資者隊伍主要由中小投資者構成,市場投機成分高,因此不會產生對現代投資理論的需求,相應地,學術界也難以對此產生研究的熱情。
然而數學技術以其精確的描述,嚴密的推導已經不容爭辯地走進了金融領域。自從1952年馬柯維茨(Markowitz)提出了用隨機變數的特徵變數來描述金融資產的收益性,不確定性和流動性以來,已經很難分清世界一流的金融雜誌是在分析金融市場還是在撰寫一篇數學論文。再回到Collins的講話,在金融證券化的趨勢中,無論是我們採用統計學的方法分析歷史數據,尋找價格波動規律,還是用數學分析的方法去複製金融產品,誰最先發現了在規律,誰就能在瞬息萬變的金融市場中獲取高額利潤。儘管由於森嚴的進入堡壘,數學進入金融領域受到了一的排斥和漠視,然而為了追求利潤,未知的恐懼顯得不堪一擊。
於是,在未來我們可以想像有這樣一個充滿美好前景的產業鏈:金融市場--金融數學--計算機技術。金融市場存在巨大的利潤和高風險,需要計算機技術幫助分析,然而計算機不可能大概,左右等描述性語言,它本質上只能識別由0和1構成的空間,金融數學在這個過程中正好扮演了一個中介角色,它可以用精確語言描述隨機波動的市場。比如,通過收益率狀態矩陣在無套利的情形下找到了無風險貼現因子。因此,金融數學能幫助IT產業向金融產業延伸,並獲取自己的利潤空間
研究科目
 金融股票
金融股票發展有價證券(尤其是期貨、期權等衍生工具)的定價理論。所用的數學方法主要是提出合適的隨機微分方程或隨機差分方程模型,形成相應的倒向方程。建立相應的非線性Feynman一Kac公式,由此導出非常一般的推廣的Black一Scho1es定價公式。所得到的倒向方程將是高維非線性帶約束的奇異方程。
研究具有不同期限和收益率的證券組合的定價問題。需要建立定價與最佳化相結合的數學模型,在數學工具的研究方面,可能需要隨機規劃、模糊規劃和最佳化算法研究。
在市場是不完全的條件下,引進與偏好有關的定價理論。
(2)不完全市場經濟均衡理論(GEI)
擬在以下幾個方面進行研究:
1.無窮維空間、無窮水平空間、及無限狀態
2.隨機經濟、無套利均衡、經濟結構參數變異、非線資產結構
3.資產證券的創新(Innovation)與設計(Design)
4.具有摩擦(Friction)的經濟
5.企業行為與生產、破產與壞債
6.證券市場博奕。
(3)GEI平板衡算法、蒙特卡羅法在經濟平衡點計算中的套用,GEI的理論在金融財政經濟巨觀經濟調控中的套用,不完全市場條件下,持續發展理論框架下研究自然資源資產定價與自然資源的持續利用。
人才現狀
 金融數學教程
金融數學教程國內開設金融數學本科專業的高等院校中,實力較強的有北京大學、復旦大學、浙江大學、山東大學、南開大學。後來從事計算機工作很出色。金融數學將後來在銀行、保險、股票、期貨領域從事研究分析,或做這些領域的軟體開發,具有很好的專業背景,而這些領域將來都很重要。國內金融數學人才鳳毛麟角,諾貝爾經濟學獎已經至少3次授予以數學為工具分析金融問題的經濟學家。北京大學金融數學系王鐸教授說,但遺憾的是,我國相關人才的培養,才剛剛起步。現在,既懂金融又懂數學的複合型人才相當稀缺。
金融數學這門新興的交叉學科已經成為國際金融界的一枝奇葩。剛剛公布的2003年諾貝爾經濟學獎,就是表彰美國經濟學家羅伯特·恩格爾和英國經濟學家克萊夫·格蘭傑分別用“隨著時間變化易變性”和“共同趨勢”兩種新方法分析經濟時間數列給經濟學研究和經濟發展帶來巨大影響。
王鐸介紹,金融數學的發展曾兩次引發了“華爾街革命”。上個世紀50年代初期,馬科威茨提出證券投資組合理論,第一次明確地用數學工具給出了在一定風險水平下按不同比例投資多種證券收益可能最大的投資方法,引發了第一次“華爾街革命”。1973年,布萊克和斯克爾斯用數學方法給出了期權定價公式,推動了期權交易的發展,期權交易很快成為世界金融市場的主要內容,成為第二次“華爾街革命”。金融數學家已經是華爾街最搶手的人才之一。最簡單的例子是,保險公司中地位和收入最高的,可能就是總精算師。美國花旗銀行副主席保爾·柯斯林著名的論斷是,“一個從事銀行業務而不懂數學的人,無非只能做些無關緊要的小事”。在美國,芝加哥大學、加州伯克利大學、史丹福大學、卡內基·梅隆大學和紐約大學等著名學府,都已經設立了金融數學相關的學位或專業證書教育。
專家認為,金融數學可能帶來的發展應該凸現在亞洲,尤其是在金融市場正在開發和具有巨大潛力的中國。香港中文大學、科技大學、城市理工大學等學校都已推出有關的訓練課程和培養計畫,並得到銀行金融業界的熱烈回響。但中國內地對該項人才的培養卻有些艱辛。王鐸介紹,國家自然科學基金委員會在一項“九五”重大項目中,列入金融工程研究內容,可以說全面啟動了國內的金融數學研究。可這比馬科威茨開始金融數學的研究套用已經晚了近半個世紀。在金融衍生產品已成為國際金融市場重要角色的背景下,我國的金融衍生產品才剛剛起步,金融衍生產品市場幾乎是空白。“加入WTO後,國際金融家們肯定將把這一系列業務帶入中國。如果沒有相應的產品和人才,如何競爭?”王鐸憂慮地說。他認為,近幾年,接連發生的墨西哥金融危機、百年老店巴林銀行倒閉等事件都在警告我們,如果不掌握金融數學、金融工程和金融管理等現代化金融技術,缺乏人才,就可能在國際金融競爭中蒙受重大損失。我們現在最缺的,就是掌握現代金融衍生工具、能對金融風險做定量分析的既懂金融又懂數學的高級複合型人才。
國內不少高校都陸續開展了與金融數學相關的教學,但畢業的學生遠遠滿足不了整個市場的需求。王鐸認為,培養這類人才還有一些難以逾越的障礙———金融數學最終要運用於實踐,可目前國內金融衍生產品市場還沒有成氣候,學生很難有實踐的機會,教和學都還是紙上談兵。另外,高校培養的人大多都是本科生,只有少量的研究生,這個領域的高端人才在國內還是鳳毛麟角。國家應該更多地關注金融和數學相結合的複合型人才的培養。王鐸回憶,1997年,北京大學建立了國內首個金融數學系時,他曾想與一些金融界人士共商辦學。但相當一部分人對此顯然並不感興趣:“什麼金融衍生產品,什麼金融數學,那都是國家應該操心的事。”
儘管當初開設金融數學系時有人認為太超前,但王鐸堅持,教育應該走在產業發展的前頭,才能為市場儲備人才。如果今天還不重視相關領域的人才培養,就可能導致我們在國際競爭中的不利。記者發現即使今天,在這個問題上,仍然一方面是高校教師對於人才稀缺的擔憂,一方面卻是一些名氣很大的專家對金融數學人才培養的冷漠。採訪中,記者多次試圖聯繫幾位國內金融數學界或金融理論界專家,可屢屢遭到拒絕。原因很簡單,他們認為,談人才培養這樣的話題太小兒科,有的甚至說,“我不了解,也根本不關注什麼人才培養”。還有的說,“我現在有很多課題要做,是我的課題重要,還是討論人才培養重要”、“我沒有時間,也沒義務向公眾解釋什麼諾貝爾經濟學獎,老百姓要不要曉得金融數學和我沒有關係”。
數據挖掘
 金融數學
金融數學1.什麼是關聯規則
在描述有關關聯規則的一些細節之前,我們先來看一個有趣的故事:"尿布與啤酒"的故事。
在一家超市里,有一個有趣的現象:尿布和啤酒赫然擺在一起出售。但是這個奇怪的舉措卻使尿布和啤酒的銷量雙雙增加了。這不是一個笑話,而是發生在美國沃爾瑪連鎖店超市的真實案例,並一直為商家所津津樂道。沃爾瑪擁有世界上最大的數據倉庫系統,為了能夠準確了解顧客在其門店的購買習慣,沃爾瑪對其顧客的購物行為進行購物籃分析,想知道顧客經常一起購買的商品有哪些。沃爾瑪數據倉庫里集中了其各門店的詳細原始交易數據。在這些原始交易數據的基礎上,沃爾瑪利用數據挖掘方法對這些數據進行分析和挖掘。一個意外的發現是:"跟尿布一起購買最多的商品竟是啤酒!經過大量實際調查和分析,揭示了一個隱藏在"尿布與啤酒"背後的美國人的一種行為模式:在美國,一些年輕的父親下班後經常要到超市去買嬰兒尿布,而他們中有30%~40%的人同時也為自己買一些啤酒。產生這一現象的原因是:美國的太太們常叮囑她們的丈夫下班後為小孩買尿布,而丈夫們在買尿布後又隨手帶回了他們喜歡的啤酒。按常規思維,尿布與啤酒風馬牛不相及,若不是藉助數據挖掘技術對大量交易數據進行挖掘分析,沃爾瑪是不可能發現數據內在這一有價值的規律的。
數據關聯是資料庫中存在的一類重要的可被發現的知識。若兩個或多個變數的取值之間存在某種規律性,就稱為關聯。關聯可分為簡單關聯、時序關聯、因果關聯。關聯分析的目的是找出資料庫中隱藏的關聯網。有時並不知道資料庫中數據的關聯函式,即使知道也是不確定的,因此關聯分析生成的規則帶有可信度。關聯規則挖掘發現大量數據中項集之間有趣的關聯或相關聯繫。Agrawal等於1993年首先提出了挖掘顧客交易資料庫中項集間的關聯規則問題,以後諸多的研究人員對關聯規則的挖掘問題進行了大量的研究。他們的工作包括對原有的算法進行最佳化,如引入隨機採樣、並行的思想等,以提高算法挖掘規則的效率;對關聯規則的套用進行推廣。關聯規則挖掘在數據挖掘中是一個重要的課題,最近幾年已被業界所廣泛研究。
 金融人才
金融人才2.關聯規則挖掘過程、分類及其相關算法
2.1關聯規則挖掘的過程
關聯規則挖掘過程主要包含兩個階段:第一階段必須先從資料集合中找出所有的高頻項目組(FrequentItemsets),第二階段再由這些高頻項目組中產生關聯規則(AssociationRules)。
關聯規則挖掘的第一階段必須從原始資料集合中,找出所有高頻項目組(LargeItemsets)。高頻的意思是指某一項目組出現的頻率相對於所有記錄而言,必須達到某一水平。一項目組出現的頻率稱為支持度(Support),以一個包含A與B兩個項目的2-itemset為例,我們可以經由公式(1)求得包含{A,B}項目組的支持度,若支持度大於等於所設定的最小支持度(MinimumSupport)門檻值時,則{A,B}稱為高頻項目組。一個滿足最小支持度的k-itemset,則稱為高頻k-項目組(Frequentk-itemset),一般表示為Largek或Frequentk。算法並從Largek的項目組中再產生Largek+1,直到無法再找到更長的高頻項目組為止。
關聯規則挖掘的第二階段是要產生關聯規則(AssociationRules)。從高頻項目組產生關聯規則,是利用前一步驟的高頻k-項目組來產生規則,在最小信賴度(MinimumConfidence)的條件門檻下,若一規則所求得的信賴度滿足最小信賴度,稱此規則為關聯規則。例如:經由高頻k-項目組{A,B}所產生的規則AB,其信賴度可經由公式(2)求得,若信賴度大於等於最小信賴度,則稱AB為關聯規則。
就沃爾馬案例而言,使用關聯規則挖掘技術,對交易資料庫中的紀錄進行資料挖掘,首先必須要設定最小支持度與最小信賴度兩個門檻值,在此假設最小支持度min_support=5%且最小信賴度min_confidence=70%。因此符合此該超市需求的關聯規則將必須同時滿足以上兩個條件。若經過挖掘過程所找到的關聯規則「尿布,啤酒」,滿足下列條件,將可接受「尿布,啤酒」的關聯規則。用公式可以描述Support(尿布,啤酒)>=5%且Confidence(尿布,啤酒)>=70%。其中,Support(尿布,啤酒)>=5%於此套用範例中的意義為:在所有的交易紀錄資料中,至少有5%的交易呈現尿布與啤酒這兩項商品被同時購買的交易行為。Confidence(尿布,啤酒)>=70%於此套用範例中的意義為:在所有包含尿布的交易紀錄資料中,至少有70%的交易會同時購買啤酒。因此,今後若有某消費者出現購買尿布的行為,超市將可推薦該消費者同時購買啤酒。這個商品推薦的行為則是根據「尿布,啤酒」關聯規則,因為就該超市過去的交易紀錄而言,支持了“大部份購買尿布的交易,會同時購買啤酒”的消費行為。
從上面的介紹還可以看出,關聯規則挖掘通常比較適用與記錄中的指標取離散值的情況。如果原始資料庫中的指標值是取連續的數據,則在關聯規則挖掘之前應該進行適當的數據離散化(實際上就是將某個區間的值對應於某個值),數據的離散化是數據挖掘前的重要環節,離散化的過程是否合理將直接影響關聯規則的挖掘結果。
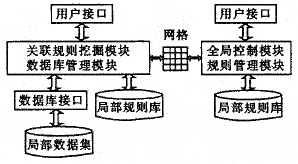 關聯規則
關聯規則2.2關聯規則的分類
按照不同情況,關聯規則可以進行分類如下:
1.基於規則中處理的變數的類別,關聯規則可以分為布爾型和數值型。
布爾型關聯規則處理的值都是離散的、種類化的,它顯示了這些變數之間的關係;而數值型關聯規則可以和多維關聯或多層關聯規則結合起來,對數值型欄位進行處理,將其進行動態的分割,或者直接對原始的數據進行處理,當然數值型關聯規則中也可以包含種類變數。例如:性別=“女”=>職業=“秘書”,是布爾型關聯規則;性別=“女”=>avg(收入)=2300,涉及的收入是數值類型,所以是一個數值型關聯規則。
2.基於規則中數據的抽象層次,可以分為單層關聯規則和多層關聯規則。
在單層的關聯規則中,所有的變數都沒有考慮到現實的數據是具有多個不同的層次的;而在多層的關聯規則中,對數據的多層性已經進行了充分的考慮。例如:IBM台式機=>Sony印表機,是一個細節數據上的單層關聯規則;台式機=>Sony印表機,是一個較高層次和細節層次之間的多層關聯規則。
3.基於規則中涉及到的數據的維數,關聯規則可以分為單維的和多維的。
在單維的關聯規則中,我們只涉及到數據的一個維,如用戶購買的物品;而在多維的關聯規則中,要處理的數據將會涉及多個維。換成另一句話,單維關聯規則是處理單個屬性中的一些關係;多維關聯規則是處理各個屬性之間的某些關係。例如:啤酒=>尿布,這條規則只涉及到用戶的購買的物品;性別=“女”=>職業=“秘書”,這條規則就涉及到兩個欄位的信息,是兩個維上的一條關聯規則。
2.3關聯規則挖掘的相關算法
1.Apriori算法:使用候選項集找頻繁項集
Apriori算法是一種最有影響的挖掘布爾關聯規則頻繁項集的算法。其核心是基於兩階段頻集思想的遞推算法。該關聯規則在分類上屬於單維、單層、布爾關聯規則。在這裡,所有支持度大於最小支持度的項集稱為頻繁項集,簡稱頻集。
該算法的基本思想是:首先找出所有的頻集,這些項集出現的頻繁性至少和預定義的最小支持度一樣。然後由頻集產生強關聯規則,這些規則必須滿足最小支持度和最小可信度。然後使用第1步找到的頻集產生期望的規則,產生只包含集合的項的所有規則,其中每一條規則的右部只有一項,這裡採用的是中規則的定義。一旦這些規則被生成,那么只有那些大於用戶給定的最小可信度的規則才被留下來。為了生成所有頻集,使用了遞推的方法。
可能產生大量的候選集,以及可能需要重複掃描資料庫,是Apriori算法的兩大缺點。
2.基於劃分的算法:Savasere等設計了一個基於劃分的算法。這個算法先把資料庫從邏輯上分成幾個互不相交的塊,每次單獨考慮一個分塊並對它生成所有的頻集,然後把產生的頻集合併,用來生成所有可能的頻集,最後計算這些項集的支持度。這裡分塊的大小選擇要使得每個分塊可以被放入主存,每個階段只需被掃描一次。而算法的正確性是由每一個可能的頻集至少在某一個分塊中是頻集保證的。該算法是可以高度並行的,可以把每一分塊分別分配給某一個處理器生成頻集。產生頻集的每一個循環結束後,處理器之間進行通信來產生全局的候選k-項集。通常這裡的通信過程是算法執行時間的主要瓶頸;而另一方面,每個獨立的處理器生成頻集的時間也是一個瓶頸。
3.FP-樹頻集算法:針對Apriori算法的固有缺陷,J.Han等提出了不產生候選挖掘頻繁項集的方法:FP-樹頻集算法。採用分而治之的策略,在經過第一遍掃描之後,把資料庫中的頻集壓縮進一棵頻繁模式樹(FP-tree),同時依然保留其中的關聯信息,隨後再將FP-tree分化成一些條件庫,每個庫和一個長度為1的頻集相關,然後再對這些條件庫分別進行挖掘。當原始數據量很大的時候,也可以結合劃分的方法,使得一個FP-tree可以放入主存中。實驗表明,FP-growth對不同長度的規則都有很好的適應性,同時在效率上較之Apriori算法有巨大的提高。
國內外套用
 金融企業
金融企業關聯規則發掘技術在國內外的套用
關聯規則挖掘技術已經被廣泛套用在西方金融行業企業中,它可以成功預測銀行客戶需求。一旦獲得了這些信息,銀行就可以改善自身行銷。現在銀行天天都在開發新的溝通客戶的方法。各銀行在自己的ATM機上就捆綁了顧客可能感興趣的本行產品信息,供使用本行ATM機的用戶了解。如果資料庫中顯示,某個高信用限額的客戶更換了地址,這個客戶很有可能新近購買了一棟更大的住宅,因此會有可能需要更高信用限額,更高端的新信用卡,或者需要一個住房改善貸款,這些產品都可以通過信用卡賬單郵寄給客戶。當客戶打電話諮詢的時候,資料庫可以有力地幫助電話銷售代表。銷售代表的電腦螢幕上可以顯示出客戶的特點,同時也可以顯示出顧客會對什麼產品感興趣。
同時,一些知名的電子商務站點也從強大的關聯規則挖掘中的受益。這些電子購物網站使用關聯規則中規則進行挖掘,然後設定用戶有意要一起購買的捆綁包。也有一些購物網站使用它們設定相應的交叉銷售,也就是購買某種商品的顧客會看到相關的另外一種商品的廣告。
但是目前在我國,“數據海量,信息缺乏”是商業銀行在數據大集中之後普遍所面對的尷尬。目前金融業實施的大多數資料庫只能實現數據的錄入、查詢、統計等較低層次的功能,卻無法發現數據中存在的各種有用的信息,譬如對這些數據進行分析,發現其數據模式及特徵,然後可能發現某個客戶、消費群體或組織的金融和商業興趣,並可觀察金融市場的變化趨勢。可以說,關聯規則挖掘的技術在我國的研究與套用並不是很廣泛深入。
關聯規則發掘技術的一些研究
由於許多套用問題往往比超市購買問題更複雜,大量研究從不同的角度對關聯規則做了擴展,將更多的因素集成到關聯規則挖掘方法之中,以此豐富關聯規則的套用領域,拓寬支持管理決策的範圍。如考慮屬性之間的類別層次關係,時態關係,多表挖掘等。近年來圍繞關聯規則的研究主要集中於兩個方面,即擴展經典關聯規則能夠解決問題的範圍,改善經典關聯規則挖掘算法效率和規則興趣性。

