術語定義
過程能力指數是指過程能力滿足產品質量標準要求(規格範圍等)的程度.
過程能力指數(Process capability index,CP或CPK)，也譯為工序能力指數、工藝能力指數、製程能力指數
什麼是過程能力指數
過程能力指數也稱工序能力指數，是指工序在一定時間裡，處於控制狀態(穩定狀態)下的實際加工能力。它是工序固有的能力，或者說它是工序保證質量的能力。這裡所指的工序，是指操作者、機器、原材料、工藝方法和生產環境等五個基本質量因素綜合作用的過程，也就是產品質量的生產過程。產品質量就是工序中的各個質量因素所起作用的綜合表現。對於任何生產過程，產品質量總是分散地存在著。若工序能力越高，則產品質量特性值的分散就會越小；若工序能力越低，則產品質量特性值的分散就會越大。那么，應當用一個什麼樣的量，來描述生產過程所造成的總分散呢?通常，都用6σ(即μ＋3σ)來表示工序能力：
| 工序能力＝6σ 若用符號P來表示工序能力，則： P＝6σ 式中：σ是處於穩定狀態下的工序的標準偏差 |
工序能力是表示生產過程客觀存在著分散的一個參數。但是這個參數能否滿足產品的技術要求，僅從它本身還難以看出。因此，還需要另一個參數來反映工序能力滿足產品技術要求(公差、規格等質量標準)的程度。這個參數就叫做工序能力指數。它是技術要求和工序能力的比值，即
| 工序能力指數=技術要求／工序能力 Cp=T/6σ T——公差 σ——總體標準差（或用樣本標準差S） |
當分布中心與公差中心重合時，工序能力指數記為Cp。當分布中心與公差中心有偏離時，工序能力指數記為Cpk。運用工序能力指數，可以幫助我們掌握生產過程的質量水平。
過程能力指數的計算公式
CPK= Min[ (USL- Mu)/3s, (Mu - LSL)/3s]
算法
計算公式
CPK= Min[ (USL- Mu)/3σ, (Mu - LSL)/3σ]
1、雙側規格
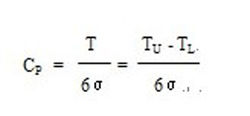過程能力指數雙側規格計算公式雙側規格情形的過程能力指數，這時，過程能力指數CP的計算公式如下：式中，T為過程統計量的技術規格的公差幅度；TU、TL分別為上、下公差界限；σ為過程統計量的總體標準差，可以在過程處於穩態時得到。
2、有偏移情形
有偏移情形的過程能力指數：當過程統計量的分布均值μ與公差中心M不重合（即有偏移）時，如圖1所示，顯然不合格率（如圖上的PU）增大，也即CP值降低，故式（1）所計算的過程能力指數不能反映有偏移的實際情形，需要加以修正。定義分布的總體均值μ與公差中心M的偏移為ε=|M-μ|，μ與M的偏移度K為：
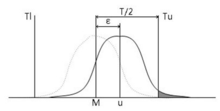有偏移情況的過程能力指數CPK這樣，當μ=M（即分布中心與公差中心重合，無偏移）時，K=0，則CPK=CP；而當μ=TU或μ=TL時，K=1，CPK=0，表示過程能力由於偏移而嚴重不足，需要採取措施加以糾正。顯然，具有：
CPK≤CP
3、單側規格
單側規格情形的過程能力指數：若只有規格上限的要求，而對規格下限無要求，則過程能力指數計算如下：
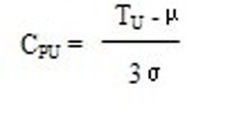單側規格過程能力指數計算公式式中，CPU為上單側過程能力指數。若μ≥TU，令CPU=0，表示過程能力嚴重不足，過程的不合格品率高達50%以上。若只有規格下限的要求。
運算方法
過程能力指數運算有5種計算方法：
直方圖（兩種繪圖方法）；
散布圖（直線回歸和曲線回歸）（5種）；
計算剩餘標準差；排列圖（自動檢索和排序）；
波動圖（單邊控制規範，也可以是雙邊控制規範）。
指標
Cp、Cpk
我們常常提到的過程能力指數Cp、Cpk是指過程的短期能力。
Cp是指過程滿足技術要求的能力，常用客戶滿意的偏差範圍除以六倍的西格瑪的結果來表示。
T=允許最大值（Tu）-允許最小值（Tl）
Cp=T/（6*σ)
所以σ越小，其Cp值越大，則過程技術能力越好。
Cpk是指過程平均值與產品標準規格發生偏移（ε）的大小，常用客戶滿意的上限偏差值減去平均值和平均值減去下限偏差值中數值小的一個，再除以三倍的西格瑪的結果來表示。
Cpk=MIN(Tu-μ，μ-Tl）/（3*σ)
或者Cpk=（1-k）*Cp，其中k=ε/（T/2）
通常狀況下，質量特性值分布的總體標準差（σ）是未知的，所以應採用樣本標準差（s）來代替。
Pp、Ppk
與Cp、Cpk不同的是， 過程能力指數Pp、Ppk是相對長期的過程能力，要求其樣本容量大，
其公式同Cp、Cpk一樣，但σ是全部樣本的標準偏差，即等於所有樣本的標準差S。
指數意義
1.67-2 過大，可適當放寬檢驗
1.33-1.67 充分，繼續保持
1-1.33 正常，但接近1危險
小於1 不充分，需改進，嚴重時停產需整頓
說明
以上所提情況皆為正態情況下，當為非正態時情況則不同。
例如：某些產品的質量特性值是遵從指數分布的，Cp=T/(5.9*σ).過程能力指數, 製程準確度, 製程精密度三者的關係Cpk = Cp * ( 1 - |Ca|)
Cpk是Ca及Cp兩者的中和反應，Ca反應的是位置關係(集中趨勢)，Cp反應的是散布關係(離散趨勢)
