定理定義
費馬平方和定理的表述是：奇質數能表示為兩個平方數之和的充分必要條件是該質數被4除餘1。
驗證推導
歐拉在1747年證明了費馬平方和定理，當年他四十歲。他在當年[[5月6日]]寄給[[哥德巴赫]]一封信，講述這個定理的證明。該證明分五步，且用到了無窮遞降法；由於信中沒有把第五步講清楚，因此[[1749年]]他再次寄給哥德巴赫一封信，詳細講述第五步的證明。
第一步
“如果兩個整數都能表示為兩個平方數之和，則它們的積也能表示為兩個平方數之和。”
第一步的證明是婆羅摩笈多－斐波那契恆等式的一種:
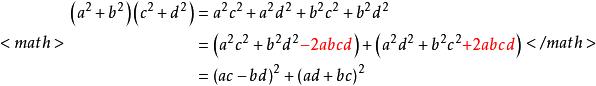費馬平方和定理
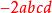費馬平方和定理
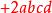費馬平方和定理
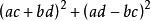費馬平方和定理而若將與·互換位置，即可得。
第二步
“如果一個能表示為兩個平方數之和的整數被另一個能表示為兩個平方數之和的素數整除，則它們的商也能表示為兩個平方數之和。”
假設a^2 + b^2能被p^2+q^2整除，且後者為素數。則p^2 + q^2能整除
:(pb-aq)(pb+aq) = p^2b^2 - a^2q^2 = p^2(a^2+b^2) - a^2(p^2+q^2).
由於p^2+q^2是素數，因此它能整除兩個因子之一。假設它能整除pb-aq。由於
:(a^2+b^2)(p^2+q^2) = (ap+bq)^2 + (aq-bp)^2\,
可推出p^2+q^2能整除(ap+bq)^2。於是等式能被p^2+q^2的平方整除。兩邊除以(p^2+q^2)^2得：
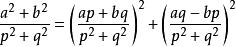費馬平方和定理因此其商能表示為兩個平方數之和。
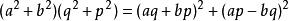費馬平方和定理如果p^2+q^2能整除pb+aq，則利用等式同樣可證。
第三步
“如果一個能表示為兩個平方數之和的整數被另一個不能表示為兩個平方數之和的整數整除，則它們的商也必有一個不能表示為兩個平方數之和的因子。”
假設x能整除a^2+b^2，且其商的分解式為p_1p_2\cdots p_n。則a^2+b^2 = x p_1p_2\cdots p_n。如果所有的因子p_i都能表示為兩個平方數之和，則我們可以用p_1、p_2、等等去除a^2+b^2，並使用第二步的結論，可得每一個商都能表示為兩個平方數之和。除到只剩x的時候，可得x也能表示為兩個平方數之和，矛盾。因此，如果x不能表示為兩個平方數之和，則至少有一個素數p_i 也不能表示為兩個平方數之和。
第四步
“如果a和b互素，則a^2 + b^2的所有因子都能表示為兩個平方數之和。”
這一步用到了無窮遞降法。設x是a^2+b^2的一個因子。可記
:a = mx \pm c,\qquad b = nx \pm d
其中c和d的絕對值最多不超過x的一半。可得：
a^2 + b^2 = m^2x^2\pm 2mxc + c^2 + n^2x^2 \pm 2nxd + d^2 = Ax + (c^2+d^2).
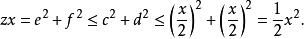費馬平方和定理因此，c^2+d^2一定能被x整除，設c^2+d^2 = yx。如果c和d不互素，則它們的[[最大公約數]]與x互質 (否則它就能整除a和b，與我們假設它們互素矛盾〕。因此它們的最大公約數的平方能整除y（因為它能整除c^2+d^2），於是我們得到e^2+f^2 = zx，其中e和f互素，且z不超過x的一半，這是因為
如果c和d互素，則我們可直接使用c和d，不必轉換成e和f。
如果x不能表示為兩個平方數之和，則根據第三步的結論，可知必有一個z的因子不能表示為兩個平方數之和；設它為w。於是我們從x推出了一個更小的整數w，都不能表示為兩個平方數之和，但都能被一個能表示為兩個平方數之和的整數整除。由於這個無窮遞降是不可能的，因此x一定能表示為兩個平方數之和。
第五步
“任何形為4n+1的素數都能表示為兩個平方數之和。”
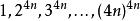費馬平方和定理如果p=4n+1，則根據費馬小定理可得被p除都餘1。因此它們的差2^{4n} -1, 3^{4n} -2^{4n},\dots,(4n)^{4n} - (4n-1)^{4n}都能被p整除。這些差可分解為a^{4n} - b^{4n} =(a^{2n}+b^{2n}/(a^{2n} - b^{2n}.
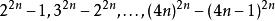費馬平方和定理由於p是素數，它一定能整除這兩個因子之一〔以下稱它們為“和因子”和“差因子”〕。如果它能整除任何一個“和因子”，則根據第四步的結論可得p能表示為兩個平方數之和〔由於a和b僅相差1，它們必然互素〕。而如果它能整除所有的4n-1個“差因子”，則它也能整除4n-2個一階差、4n-3個二階差，依此類推。由於數列1^k, 2^k, 3^k,\dots的第k階差都等於k!，於是第2n階差都等於(2n)!，顯然它不能被p整除。因此，p不能整除所有的“差因子”，得證p能表示為兩個平方數之和。
