基本內容
注意有些整數不可表示為3個整數的平方和，例如7。
歷史
1743年，瑞士數學家歐拉發現了一個著名的恆等式：
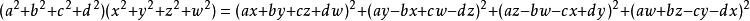拉格朗日四平方和定理
拉格朗日四平方和定理
拉格朗日四平方和定理
拉格朗日四平方和定理根據上述歐拉恆等式或四元數的概念可知如果正整數和能表示為4個整數的平方和，則其乘積也能表示為4個整數的平方和。於是為證明原命題只需證明每個素數可以表示成4個整數的平方和即可。
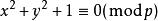拉格朗日四平方和定理
拉格朗日四平方和定理
拉格朗日四平方和定理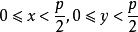
拉格朗日四平方和定理1751年，歐拉又得到了另一個一般的結果。即對任意奇素數，同餘方程必有一組整數解滿足（引理）。
至此，證明四平方和定理所需的全部引理已經全部證明完畢。此後，拉格朗日和歐拉分別在1770年和1773年作出最後的證明。
證明
根據上面的四平方和恆等式及算術基本定理，可知只需證明質數可以表示成四個整數的平方和即可。
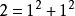拉格朗日四平方和定理，因此只需證明奇質數可以表示成四個整數的平方和。
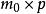拉格朗日四平方和定理
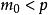拉格朗日四平方和定理顯然，奇質數p必有正倍數可以表示成四個整數的平方和（如4p^2)。在這些倍數中，必存在一個 最小的。設該數為。又從引理可知。
證明m0不會是偶數
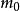拉格朗日四平方和定理
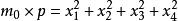拉格朗日四平方和定理
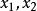拉格朗日四平方和定理
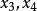拉格朗日四平方和定理
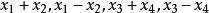拉格朗日四平方和定理設是偶數，且。由奇偶性可得知必有兩個數或四個數的奇偶性相同。不失一般性設的奇偶性相同，的奇偶性相同，均為偶數，可得出公式：
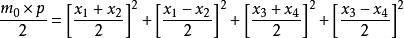拉格朗日四平方和定理
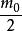拉格朗日四平方和定理 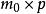拉格朗日四平方和定理是正整數使得假設可以表示成四個整數的平方和不符。
證明m0=1
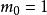拉格朗日四平方和定理
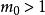拉格朗日四平方和定理現在用反證法證明。設。
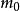拉格朗日四平方和定理不可整除xj的最大公因子，否m0^2可整除m0p，則得m0是p的因子，但1 < m0 < p且p為質數，矛盾。 故存在不全為零、絕對值小m0/2（注意m0是奇數在此的重要性）整數的y1,y2,y3,y4使得 yyj= xj(mod m0)。
0<∑yi^2<4(m0/2)^2=m0^2∑yi^2≡∑xi^2≡0(modm0)可得∑yi^2=m0m1，其中m0是正整數且小於m0。
下面證明m1p可以表示成四個整數的平方和，從而推翻假設。 用四平方和恆等式令∑zi^2=∑yi^2*∑xi^2，可知zj是m0的倍數，令zj= m0tj,
∑zi^2=∑yi^2*∑xi^2m0^2∑ti^2=m0m1m0p∑ti^2=m1p<m0p矛盾。
引理的證明
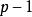拉格朗日四平方和定理
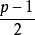拉格朗日四平方和定理
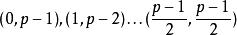拉格朗日四平方和定理將和為的剩餘系兩個一組的分開，可得出組，分別為。
拉格朗日四平方和定理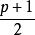
拉格朗日四平方和定理
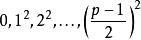拉格朗日四平方和定理將模的二次剩餘有個，分別為。
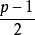拉格朗日四平方和定理 拉格朗日四平方和定理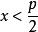
拉格朗日四平方和定理
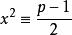拉格朗日四平方和定理
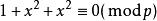拉格朗日四平方和定理若是模的二次剩餘，選取使得則，定理得證。
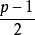拉格朗日四平方和定理 拉格朗日四平方和定理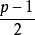 拉格朗日四平方和定理
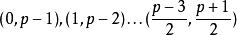拉格朗日四平方和定理若不屬於模的二次剩餘，則剩下組，分別為，而模p的二次剩餘仍有(p+1)/2個，由於(p+1)/2>(p-1)/2 ，根據抽屜原理，存在
