定義
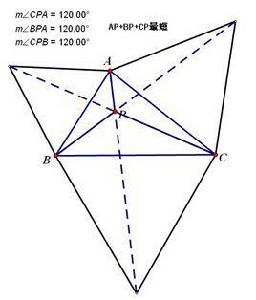
1.若三角形3個內角均小於120°,那么3條距離連線正好三等分費馬點所在的周角,即該點所對三角形三邊的張角相等,均為120 °。所以三角形的費馬點也稱為三角形的 等角中心。
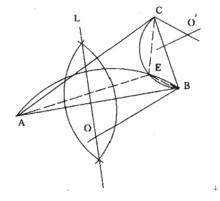
(托里拆利的解法中對這個點的描述是:對於每一個角都小於120°的三角形ABC的每一條邊為底邊,向外作正三角形,然後作這三個正三角形的外接圓。托里拆利指出這三個外接圓會有一個共同的交點,而這個交點就是所要求的點。這個點和當時已知的三角形特殊點都不一樣。這個點因此也叫做托里拆利點。)
2.若三角形有一內角大於等於120 °,則此鈍角的頂點就是距離和最小的點。
相關計算
 費馬點
費馬點 費馬點
費馬點 費馬點
費馬點 費馬點
費馬點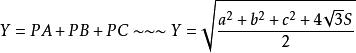 費馬點
費馬點S為面積
尺規作圖法
 費馬點
費馬點(1)根據定義,首先判斷給定三角形的三個內角是否均小於120°.
1.以任意半徑畫圓0,並作出圓的一條直徑AB。
2.以點A(或點B)為圓心,OA(或OB)為半徑畫出圓A(或圓B)
3.兩圓相交於C點,聯結AC,BC
4.則∠CBA或∠CAB為30°,∠C為90°,兩角相加即為120°
(2)若大於等於120°,則該鈍角頂點即為該三角形的費馬點
 費馬點
費馬點(3)若三角形的三個角均小於120°,則繼續做以下步驟
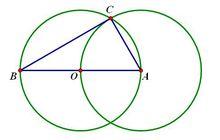
1.以三角形任意一邊a向外做等邊三角形
2.找出該等邊三角形的外心,並作出外接圓
3.聯結a邊所對的兩個頂點(連線AD)
4.該連線與外接圓交點即為該三角形的費馬點
【步驟3證明】
如圖,E,B,D,C 四點共圓,∠D=60°,所以∠BEC=180°-∠D=120°
弧BD所對的圓周角∠BED=∠BCD=60°,所以∠AEB=120°
1.如圖,E,B,D,C 四點共圓,∠D=60°,所以∠BEC=180°-∠D=120°
2.弧BD所對的圓周角∠BED=∠BCD=60°,所以∠AEB=120°
向量表示
F為三角形ABC的費馬點,O為任意一點,則
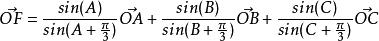 費馬點
費馬點判定
 費馬點的計算
費馬點的計算(1)對於任意三角形△ABC內或三角形上某一點E,若EA+EB+EC有最小值,則取到最小值時E為費馬點。
三角形費馬點
法一:
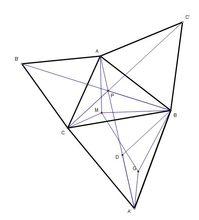
如右圖,在△ABC中,P為其中任意一點。連線AP,BP,得到△ABP。
以 點B為鏇轉中心,將 △ABP逆時針鏇轉 60°,得到△EBD
∵鏇轉60°,且BD=BP,
∴△DBP 為一個等邊三角形
∴PB=PD
因此, PA+PB+PC=DE+PD+PC
由此可知當E、D、P、C 四點共線時, 為PA+PB+PC最小
若E、D、P共線時,
∵等邊△DBP
∴∠EDB=120°
同理,若D、P、C共線時,則 ∠CPB=120°
∴P點為滿足∠APB=∠BPC=∠APC=120° 的點。
法二:
如圖,以△ABC三邊為邊向外作等邊△ABD、△BCE、△ACF,
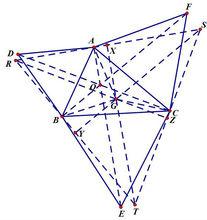 費馬點
費馬點連線CD、BF、AE交於點O,試證:O是費馬點。
證明:在△ACD、△ABF中,
AD=AB
∠DAC=∠BAF
AC=AF
∴△ACD≌△ABF(SAS)
∴∠ADC=∠ABF
∴A、B、O、D四點共圓。
∴∠AOB=120°。
同理可得,∠AOB=∠AOC=∠BOC=120°。
過點A、B、C作OA、OB、OC的垂線交於三點R、S、T,易知△RST
是正三角形。
在△ABC內作異於O一點G,作RS、ST、RT的垂線GX、GY、GZ,連
接GA、GB、GC。
易用面積法得:OA+OB+OC=GX+GY+GZ。
∵點到線之間,垂線段最短,
∴OA+OB+OC=GX+GY+GZ<GA+GB+GC
∴點O是費馬點。
四邊形費馬點
平面四邊形中費馬點證明相對於三角形中較為簡易,也較容易研究。
(1)在凸四邊形ABCD中,費馬點為兩對角線AC、BD交點P。
(2)在凹四邊形ABCD中,費馬點為凹頂點D(P)。
 平面四邊形費馬點證明圖形
平面四邊形費馬點證明圖形經過上述的推導,我們即得出了三角形中費馬點的找法:當三角形有一個內角大於或等於120°的時候,費馬點就是這個內角的頂點;如果三個內角都在120°以內,那么,費馬點就是使得費馬點與三角形三頂點的連線兩兩夾角為120°的點。另一種更為簡捷的證明 :設O為三頂點連線最短點,以A為圓心AO為半徑做圓P。將圓P視作一面鏡子。顯然O點應該為B出發的光線經過鏡子到C的反射點(如果不是,反射點為O',就會有BO’+ CO' < BO+ CO,而AO’= AO,就會有 AO’+ BO’+ CO' < AO + BO + CO)。
不失一般性。O點對於B、C為圓心的鏡子也成立。因此根據對稱性AO、BO、CO之間夾角都是120°
(補充說明:AO、BO、CO是每個鏡子的法線)
 費馬點
費馬點Ps:費馬點是到三角形三個頂點距離的和最小的點;
而三角形的重心是到三角形三個頂點距離的平方和最小的點。
要有所區別
歷史背景
皮耶·德·費馬(Pierre de Fermat)是一個17世紀的法國律師,也是一位業餘數學家。之所以稱業餘,是由於皮耶·德·費馬具有律師的全職工作。他的姓氏根據法文與英文實際發音也常譯為“費爾瑪”(注意“瑪”字)。費馬最後定理在中國習慣稱為費馬大定理,西方數學界原名“最後”的意思是:其它猜想都證實了,這是最後一個。
著名的數學史學家貝爾(E. T. Bell)在20世紀初所撰寫的著作中,稱皮耶·德·費馬為”業餘數學家之王“。貝爾深信,費馬比皮耶·德·費馬同時代的大多數專業數學家更有成就,然而皮耶·德·費馬並未在其他方面另有成就,本人也漸漸退出人們的視野,考慮到17世紀是傑出數學家活躍的世紀,因而貝爾認為費馬是17世紀數學家中最多產的明星。
費馬點問題最早是由法國數學家皮埃爾·德·費馬在一封寫給義大利數學家埃萬傑利斯塔·托里拆利(氣壓計的發明者)的信中提出的。托里拆利最早解決了這個問題,而19世紀的數學家斯坦納重新發現了這個問題,並系統地進行了推廣,因此這個點也稱為 托里拆利點或 斯坦納點,相關的問題也被稱作 費馬-托里拆利-斯坦納問題。這一問題的解決極大推動了聯合數學的發展,在近代數學史上具有里程碑式的意義。