家族簡介
在科學史上,父子科學家、兄弟科學家並不鮮見,然而,在一個家族跨世紀的幾代人中,眾多父子兄弟都是科學家的較為罕見,其中,瑞士的伯努利(也譯作貝努力、伯努利)家族最為突出。
 貝努利
貝努利伯努利家族3代人中產生了8位科學家,出類拔萃的至少有3位;而在他們一代又一代的眾多子孫中,至少有一半相繼成為傑出人物。伯努利家族的後裔有不少於120位被人們系統地追溯過,他們在數學、科學、技術、工程乃至法律、管理、文學、藝術等方面享有名望,有的甚至聲名顯赫。最不可思議的是這個家族中有兩代人,他們中的大多數數學家,並非有意選擇數學為職業,然而卻忘情地沉溺於數學之中,有人調侃他們就像酒鬼碰到了烈酒。
老尼古拉·伯努利(Nicolaus Bernoulli,公元1623~1708年)生於巴塞爾,受過良好教育,曾在當地政府和法務部門任高級職務。他有3個有成就的兒子。其中長子雅各布(Jocob,公元1654~1705年)和第三個兒子約翰(Johann,公元1667~1748年)成為著名的數學家,第二個兒子小尼古拉(Nicolaus I,公元1662~1716年)在成為彼得堡科學院數學界的一員之前,是伯爾尼的第一個法律學教授。
雅各布
1654年12月27日,雅各布·伯努利生於巴塞爾,畢業於巴塞爾大學,1671年17歲時獲藝術碩士學位。這裡的藝術指“自由藝術”,包括算術、幾何學、天文學、數理音樂和文法、修辭、雄辯術共7大門類。遵照父親的願望,他於1676年22歲時又取得了神學碩士學位。然而,他也違背父親的意願,自學了數學和天文學。1676年,他到日內瓦做家庭教師。從1677年起,他開始在那裡寫內容豐富的《沉思錄》。
1678年和1681年,雅各布·伯努利兩次外出旅行學習,到過法國、荷蘭、英國和德國,接觸和交往了許德、玻意耳、胡克、惠更斯等科學家,寫有關於彗星理論(1682年)、重力理論(1683年)方面的科技文章。1687年,雅各布在《教師學報》上發表數學論文《用兩相互垂直的直線將三角形的面積四等分的方法》,同年成為巴塞爾大學的數學教授,直至1705年8月16日逝世。
1699年,雅各布當選為巴黎科學院外籍院士;1701年被柏林科學協會(後為柏林科學院)接納為會員。
許多數學成果與雅各布的名字相聯繫。例如懸鏈線問題(1690年),曲率半徑公式(1694年),“伯努利雙紐線”(1694年),“伯努利微分方程”(1695年),“等周問題”(1700年)等。
雅各布對數學最重大的貢獻是在機率論研究方面。他從1685年起發表關於賭博遊戲中輸贏次數問題的論文,後來寫成巨著《猜度術》,這本書在他死後8年,即1713年才得以出版。
最為人們津津樂道的軼事之一,是雅各布醉心於研究對數螺線,這項研究從1691年就開始了。他發現,對數螺線經過各種變換後仍然是對數螺線,如它的漸屈線和漸伸線是對數螺線,自極點至切線的垂足的軌跡,以極點為發光點經對數螺線反射後得到的反射線,以及與所有這些反射線相切的曲線(回光線)都是對數螺線。他驚嘆這種曲線的神奇,竟在遺囑里要求後人將對數螺線刻在自己的墓碑上,並附以頌詞“縱然變化,依然故我”,用以象徵死後永生不朽。
約翰
雅各布·伯努利的弟弟約翰·伯努利比哥哥小13歲,1667年8月6日生於巴塞爾,1748年1月1日卒於巴塞爾,享年81歲,而哥哥只活了51歲。
約翰於1685年18歲時獲巴塞爾大學藝術碩士學位,這點同他的哥哥雅各布一樣。他們的父親老尼古拉要大兒子雅各布學法律,要小兒子約翰去學經商。但約翰在雅各布的帶領下進行反抗,去學習醫學和古典文學。約翰於1690年獲醫學碩士學位,1694年又獲得博士學位。但他發現他骨子裡的興趣是數學。他一直向雅各布學習數學,並頗有造詣。1695年,28歲的約翰取得了他的第一個學術職位——荷蘭格羅寧根大學數學教授。10年後的1705年,約翰接替去世的雅各布任巴塞爾大學數學教授。同他的哥哥一樣,他也當選為巴黎科學院外籍院士和柏林科學協會會員。1712、1724和1725年,他還分別當選為英國皇家學會、義大利波倫亞科學院和彼得堡科學院的外籍院士。
約翰的數學成果比雅各布還要多。例如解決懸鏈線問題(1691年),提出洛必達法則(1694年)、最速降線(1696年)和測地線問題(1697年),給出求積分的變數替換法(1699年),研究弦振動問題(1727年),出版《積分學教程》(1742年)等。
約翰與他同時代的110位學者有通信聯繫,進行學術討論的信件約有2500封,其中許多已成為珍貴的科學史文獻,例如同他的哥哥雅各布以及萊布尼茨、惠更斯等人關於懸鏈線、最速降線(即鏇輪線)和等周問題的通信討論,雖然相互爭論不斷,特別是約翰和雅各布互相指責過於尖刻,使兄弟之間時常造成不快,但爭論無疑會促進科學的發展,最速降線問題就導致了變分法的誕生。
約翰的另一大功績是培養了一大批出色的數學家,其中包括18世紀最著名的數學家歐拉、瑞士數學家克萊姆、法國數學家洛必達,以及他自己的兒子丹尼爾和侄子尼古拉二世等。
丹尼爾
生平簡介
丹尼爾·伯努利,(Daniel Bernoulli 1700~1782)瑞士物理學家、數學家、醫學家。1700年2月8日生於荷蘭格羅寧根。著名的伯努利家族中最傑出的一位。他是數學家J.伯努利的次子,和他的父輩一樣,違背家長要他經商的願望,堅持學醫,他曾在海得爾貝格、斯脫思堡和巴塞爾等大學學習哲學、倫理學、醫學。1721年取得醫學碩士學位。伯努利在25歲時(1725)就應聘為聖彼得堡科學院的數學院士。8年後回到瑞士的巴塞爾,先任解剖學教授,後任動力學教授,1750年成為物理學教授。
在1725~1749年間,伯努利曾十次榮獲法國科學院的年度獎。
1782年3月17日,伯努利在瑞士巴塞爾逝世,終年82歲。
約翰·伯努利想迫使他的第二個兒子丹尼爾去經商,但丹尼爾在不由自主地陷進數學之前,曾寧可選擇醫學成為醫生。
丹尼爾(Daniel,公元1700~1782年)出生於荷蘭的格羅寧根,1716年16歲時獲藝術碩士學位;1721年又獲醫學博士學位。他曾申請解剖學和植物學教授職位,但未成功。
丹尼爾受父兄影響,一直很喜歡數學。1724年,他在威尼斯旅途中發表《數學練習》,引起學術界關注,並被邀請到聖彼得堡科學院工作。同年,他還用變數分離法解決了微分方程中的里卡提方程。1725年,25歲的丹尼爾受聘為聖彼得堡的數學教授。1727年,20歲的歐拉(後人將他與阿基米德、艾薩克·牛頓、高斯並列為數學史上的“四傑”),到聖彼得堡成為丹尼爾的助手。
然而,丹尼爾認為聖彼得堡那地方的生活比較粗鄙,以至於8年以後的1733年,他找到機會返回巴塞爾,終於在那兒成為解剖學和植物學教授,最後又成為物理學教授。
1734年,丹尼爾榮獲巴黎科學院獎金,以後又10次獲得該獎金。能與丹尼爾媲美的只有大數學家歐拉。丹尼爾和歐拉保持了近40年的學術通信,在科學史上留下一段佳話。
在伯努利家族中,丹尼爾是涉及科學領域較多的人。他出版了經典著作《流體動力學》(1738年);研究彈性弦的橫向振動問題(1741~1743年),提出聲音在空氣中的傳播規律(1762年)。他的論著還涉及天文學(1734年)、地球引力(1728年)、湖汐(1740年)、磁學(1743、1746年),振動理論(1747年)、船體航行的穩定(1753、1757年)和生理學(1721、1728年)等。丹尼爾的博學成為伯努利家族的代表。
丹尼爾於1747年當選為柏林科學院院士,1748年當選巴黎科學院院士,1750年當選英國皇家學會會員。他一生獲得過多項榮譽稱號。
科學成就
1.在物理學上的貢獻有:
(1)1738年出版了《流體動力學》一書,共13章。這是他最重要的著作。書中用能量守恆定律解決流體的流動問題,寫出了流體動力學的基本方程,後人稱之為“伯努利方程”,提出了“流速增加、壓強降低”的伯努利原理。
(2)他還提出把氣壓看成氣體分子對容器壁表面撞擊而生的效應,建立了分子運動理論和熱學的基本概念,並指出了壓強和分子運動隨溫度增高而加強的事實。
(3)從1728年起,他和歐拉還共同研究柔韌而有彈性的鏈和梁的力學問題,包括這些物體的平衡曲線,還研究了弦和空氣柱的振動。
(4)他曾因天文測量、地球引力、潮汐、磁學、洋流、船體航行的穩定、土星和木星的不規則運動和振動理論等成果而獲獎。
2.在數學方面,有關微積分、微分方程和機率論等,他也做了大量而重要的工作。
伯努利定律
 貝努利
貝努利在一個流體系統,比如氣流、水流中,流速越快,流體產生的壓力就越小,這就是被稱為“流體力學之父”的丹尼爾·伯努利1738年發現的“伯努利定律”。這個壓力產生的力量是巨大的,空氣能夠托起沉重的飛機,就是利用了伯努利定律。飛機機翼的上表面是流暢的曲面,下表面則是平面。這樣,機翼上表面的氣流速度就大於下表面的氣流速度,所以機翼下方氣流產生的壓力就大於上方氣流的壓力,飛機就被這巨大的壓力差“托住”了。當然了,這個壓力到底有多大,一個高深的流體力學公式“伯努利方程”會去計算它。
方程式
v=流動速度
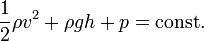 伯努利定律
伯努利定律g=地心加速度(地球)
h=流體處於的高度(從某參考點計)
p=流體所受的壓強
ρ=流體的密度
伯努利方程
伯努利理想正壓流體在有勢徹體力作用下作定常運動時,運動方程(即歐拉方程)沿流線積分而得到的表達運動流體機械能守恆的方程。因著名的瑞士科學家D.伯努利於1738年提出而得名。對於重力場中的不可壓縮均質流體 ,方程為p+ρgz+(1/2)*ρv^2=C 式中p、ρ、v分別為流體的壓強、密度和速度;z 為鉛垂高度;g為重力加速度。
上式各項分別表示單位體積流體的壓力能 p、重力勢能ρg z和動能(1/2)*ρv ^2,在沿流線運動過程中,總和保持不變,即總能量守恆。但各流線之間總能量(即上式中的常量值)可能不同。對於氣體,可忽略重力,方程簡化為p+(1/2)*ρv ^2=常量(p0),各項分別稱為靜壓 、動壓和總壓。顯然 ,流動中速度增大,壓強就減小;速度減小, 壓強就增大;速度降為零,壓強就達到最大(理論上應等於總壓)。飛機機翼產生舉力,就在於下翼面速度低而壓強大,上翼面速度高而壓強小 ,因而合力向上。 據此方程,測量流體的總壓、靜壓即可求得速度,成為皮托管測速的原理。在無鏇流動中,也可利用無鏇條件積分歐拉方程而得到相同的結果但涵義不同,此時公式中的常量在全流場不變,表示各流線上流體有相同的總能量,方程適用於全流場任意兩點之間。在粘性流動中,粘性摩擦力消耗機械能而產生熱,機械能不守恆,推廣使用伯努利方程時,應加進機械能損失項。
伯努利效應
1726年,伯努利通過無數次實驗,發現了“邊界層表面效應”:流體速度加快時,物體與流體接觸的界面上的壓力會減小,反之壓力會增加。為紀念這位科學家的貢獻,這一發現被稱為“伯努利效應”。伯努利效應適用於包括氣體在內的一切流體,是流體作穩定流動時的基本現象之一,反映出流體的壓強與流速的關係,流速與壓強的關係:流體的流速越大,壓強越小;流體的流速越小,壓強越大。
比如,管道內有一穩定流動的流體,在管道不同截面處的豎直開口細管內的液柱的高度不同,表明在穩定流動中,流速大的地方壓強小,流速小的地方壓強大。這一現象稱為“伯努利效應”。伯努利方程:p+1/2pv^2=常量。
在列車站台上都劃有安全線。這是由於列車高速駛來時,靠近列車車廂的空氣將被帶動而運動起來,壓強就減小,站台上的旅客若離列車過近,旅客身體前後出現明顯壓強差,將使旅客被吸向列車而受傷害。
伯努利效應的套用舉例:飛機機翼、 噴霧器、汽油發動機的汽化器、球類比賽中的鏇轉球。
伯努利數
伯努利數是18世紀瑞士數學家雅各布·伯努利引入的一個數。設伯努利數為B(n),它的定義為: t/(e^t-1)=∑[B(n)*(t^n)/(n!)](n:0->∞) 這裡|t|<2。由計算得B(0)=1,B(1)=-1/2,B(2)=1/6,B(3)=0,B(4)=-1/30,B(5)=0,B(6)=1/42,B(7)=0, B(8)=-1/30,B(9)=0),B(10)=5/66,B(11)=0,B(12)=-691/2730,B(13)=0,B(14)=7/6,B(15)=0,B(16)=-3617/510,B(17)=0, B(18)=43867/798,B(19)=0, B(20)=-174611/330 …… 一般地,n>=1時,有B(2n+1)=0;n>=2時,有公式B(n)=∑[C(k,n)*B(k)](k:0->n)可用來逐一計算伯努利數。伯努利數在數論中很有用。例如,對於佩爾方程-=-4(≡1(mod4)是素數),N.C.安克尼和E.阿廷曾猜想它的最小解x0+(y0)*√(p)滿足 ,1960年,L.J.莫德爾證明了在≡5(mod8)時,S.喬拉證明了在≡1(mod8)時,上述猜想等價於伯努利數B((p-1)/2)的分子不被整除。伯努利數還可用於費馬大定理的論證中。設>3,如果伯努利數B,B,…,B(p-3)的每一個的分子不被整除,這樣的素數叫正規素數,否則就叫非正規素數。德國數學家E.E.庫默爾證明了:當為正規素數時,費馬大定理成立。不難計算當3<<100時,除開=37,59,67以外,其餘的素數都是正規素數。因此,在費馬大定理的研究中,庫默爾的結果是一項突破性的工作(見不定方程)。儘管有許多判別正規素數的法則,但是,是否有無窮多個正規素數,尚未解決。而非正規素數有無窮多個,早在1915年就被人們所證明。
相關軼事
著名的伯努利家族曾產生許多傳奇和軼事。對於這樣一個既有科學天賦然而又語言粗暴的家族來說,這似乎是很自然的事情。一個關於丹尼爾的傳說是這樣的:有一次在旅途中,年輕的丹尼爾同一個風趣的陌生人閒談,他謙虛地自我介紹說:“我是丹尼爾·伯努利。”陌生人立即帶著譏諷的神情回答道:“那我就是艾薩克·牛頓!”

