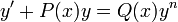簡介
形如y'+P（x）=Q（x）y^n的微分方程，稱為伯努利微分方程，其中n≠0並且n≠1 ，其中P（x），Q（x）為已知函式，因為當n=0，1時該方程是線性微分方程。它以雅各布·伯努利（Jacob Bernoulli）命名，他在1695年進行了研究。伯努利方程是特殊的，因為它們是具有已知精確解的非線性微分方程。 伯努利方程的著名特殊情況是邏輯微分方程。
轉換為線性微分方程
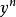伯努利微分方程伯努利微分方程可以把變數替換成為線性微分方程，將伯努利微分方程兩端除以，得
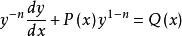伯努利微分方程
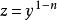伯努利微分方程
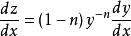伯努利微分方程作變數替換，則。代入上式，有：
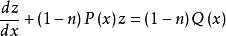伯努利微分方程 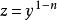伯努利微分方程這是以z為未知函式的一階線性微分方程，由此方程解出z，再由可得伯努利微分方程的解。
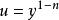伯努利微分方程注意，對於n=0和n = 1，伯努利方程是線性的。 對於n≠0和n≠1，替換 將任何伯努利方程調整到線性微分方程。 例如：
讓我們考慮以下微分方程：
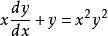伯努利微分方程以伯努利形式（用n = 2））重寫它：
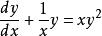伯努利微分方程
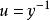伯努利微分方程現在，用 我們得到：
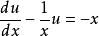伯努利微分方程，它是一個線性微分方程。
求解
伯努利微分方程作為線性微分方程的解：
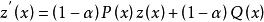伯努利微分方程那么我們有
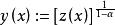伯努利微分方程是下面方程的解
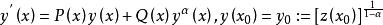伯努利微分方程
伯努利微分方程對於每個這樣的微分方程，都有>0，我們有y恆等於0。
