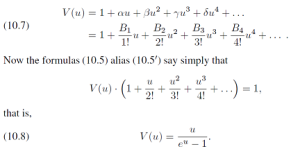定義
在數學上,伯努利數是一個有理數數列,在許多領域都有很大的套用。其定義方式也是多種多樣,最常見的有以下兩種定義方式。
生成函式定義
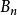 伯努利數
伯努利數設伯努利數為 ,他用很多種定義方式,其中利用生成函式定義為:
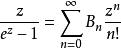 伯努利數
伯努利數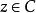 伯努利數
伯努利數這裡 。 ,利用生成函式定義,我們可以計算前9項伯努利數。列舉如下:
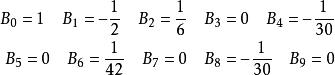 伯努利數
伯努利數 伯努利數
伯努利數 伯努利數
伯努利數注意到,當 為奇數的時候,除了 以外,其餘都是0。
 伯努利數
伯努利數 伯努利數
伯努利數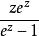 伯努利數
伯努利數(其中 在某些書本上採用 ,只需將生成函式改為 )
遞歸定義
利用遞歸定義伯努利數:
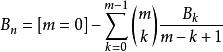 伯努利數
伯努利數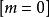 伯努利數
伯努利數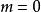 伯努利數
伯努利數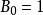 伯努利數
伯努利數其中 表示當 時,取1,其餘取0。 。
解釋
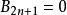 伯努利數
伯努利數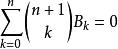 伯努利數
伯努利數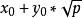 伯努利數
伯努利數一般地,n≥1時,有 ;n≥2時,有公式 可用來逐一計算伯努利數。伯努利數在數論中很有用。例如,對於佩爾方程-=-4(≡1(mod4)是素數),N.C.安克尼和E.阿廷曾猜想它的最小解滿足,1960年,L.J.莫德爾證明了在≡5(mod8)時,S.喬拉證明了在≡1(mod8)時,上述猜想等價於伯努利數B((p-1)/2)的分子不被整除。伯努利數還可用於費馬大定理的論證中。設n>3,如果伯努利數B,B,…,B(p-3)的每一個的分子不被整除,這樣的素數叫正規素數,否則就叫非正規素數。
重要套用
求前n項和
在求前n項和的方法上,利用Bernoulli生成函式的定義,我們可以得出一般的p次方前n項和公式,自然,在證明過程中伯努利數有重大的作用。
要求下式的前n項和:
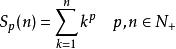 伯努利數
伯努利數如:
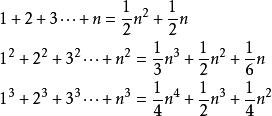 伯努利數
伯努利數下面我們來推導一般公式:
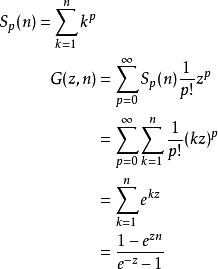 伯努利數
伯努利數注意到伯努利數的生成函式定義,我們有:
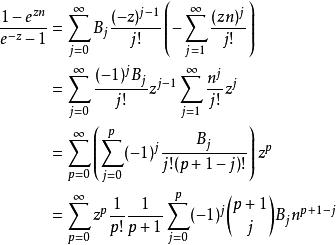 伯努利數
伯努利數對照係數即得:
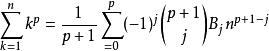 伯努利數
伯努利數證畢。
判別素數
德國數學家E.E.庫默爾證明了:當為正規素數時,費馬大定理成立。不難計算當3<<100時,除開37,59,67以外,其餘的素數都是正規素數。因此,在費馬大定理的研究中,庫默爾的結果是一項突破性的工作(見不定方程)。儘管有許多判別正規素數的法則,但是,是否有無窮多個正規素數,尚未解決。而非正規素數有無窮多個,早在1915年就被人們所證明。
 伯努利數
伯努利數 伯努利數
伯努利數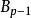 伯努利數
伯努利數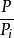 伯努利數
伯努利數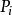 伯努利數
伯努利數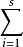 伯努利數
伯努利數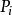 伯努利數
伯努利數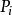 伯努利數
伯努利數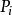 伯努利數
伯努利數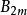 伯努利數
伯努利數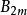 伯努利數
伯努利數根據等冪和與判別素數的充要條件,獲得了伯努利數與判別素數的充要條件,並利用所得結果對居加猜想進行了討論,證明了:若(P-1)≡-1(modp)成立,則P是素數或者P=P1、P2…PS是絕對偽素數,並且P||的分母,P|(P||+1)的分子;≡1(mod);1/-1/P是整數;在2≤2m≤(p/5-1)內必存在偶數2m,使得對每個均有-1|2m,P|的分母,P|(P+1)的分子。
c++代碼
double Bernoulli(int x)//伯努利數
{
int k=x;
double B=0;
if(x==0)
{
return 1;
}
else
{
if(x>1&&x%2==1)
{
return 0;
}
else
{
while(k)
{
k--;
B += -1.0 * ( Factorial(x) * Bernoulli(k) )/( Factorial(x-k) * Factorial(k) * (x-k+1) ) ;
}
return B;
}
}
}
double Factorial(int x)//階乘
{
if(x==1||x==0)
return 1;
else
return 1.0*x*Factorial(x-1);
}