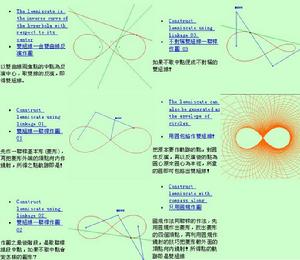伯努利雙紐線

伯努利雙紐線，描述首見於1694年雅各布·伯努利將其作為橢圓的一種類比來處理。橢圓是由到兩個定點距離之和為定值的點的軌跡。而卡西尼卵形線則是由到兩定點距離之乘積為定值的點的軌跡。當此定值使得軌跡經過兩定點的中點時，軌跡便為伯努利雙紐線。伯努利將這種曲線稱為lemniscate，為拉丁文中“懸掛的絲帶”之意。伯努利雙紐線在科技和輕工業領域也得到了廣泛套用，伯努利還將伯努利雙紐線套用於賭博術中。

基本內容

設定線段AB長度為2a,動點M滿足

MA·MB=a^2

那么M的軌跡稱為伯努利雙紐線（Lemniscate of Bernoulli）

其方程為

(

+

) = 2

(

−

)

極坐標方程:

ρ^2=a^2·sin2θ (左圖)

和ρ^2=a^2·cos2θ (右圖)

求雙紐線的弧長需要套用橢圓積分。雙紐線可視為雙曲線的反演變換，反演圓心在雙曲線焦點的中點。

伯努利雙紐線