統計學定義
二項分布與生活息息相關醫學領域定義
二項分布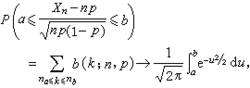
二項分布公式P=C(X,n)*π^X*(1-π)^(n-X)
式中的n為獨立的伯努利試驗次數，π為成功的機率，（1-π）為失敗的機率，X為在n次伯努里試驗中出現成功的次數，表示在n次試驗中出現X的各種組合情況，在此稱為二項係數（binomial coefficient）。
所以的含義為：含量為n的樣本中，恰好有X例陽性數的機率。
概念
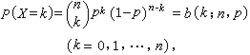二項分布公式P(ξ=K)=C(n,k)*p^k*(1-p)^(n-k),其中C(n,k)=n!/(k!*(n-k)!)注意！:第二個等號後面的括弧里的是上標，表示的是方冪。
那么就說這個屬於二項分布。
其中P稱為成功機率。
記作ξ~B(n,p)期望：Eξ=np
方差:Dξ=npq
其中q=1-p
證明:由二項式分布的定義知，隨機變數X是n重伯努利實驗中事件A發生的次數，且在每次試驗中A發生的機率為p.因此，可以將二項式分布分解成n個相互獨立且以p為參數的（0-1）分布隨機變數之和.
設隨機變數X（k）(k=1,2,3...n)服從（0-1）分布，則X=X(1)+X(2)+X(3)....X(n).
因X(k)相互獨立,所以期望：E(X)=E[X(1)+X(2)+X(3)....X(n)]=np.
方差：D(X)=D[X(1)+X(2)+X(3)....X(n)]=np(1-p).
證畢.
以上證明摘自高等教育出版社《機率論與數理統計》第四版
如果
1．在每次試驗中只有兩種可能的結果，而且是互相對立的；
2．每次實驗是獨立的,與其它各次試驗結果無關;
3．結果事件發生的機率在整個系列試驗中保持不變，則這一系列試驗稱為伯努利實驗。
二項分布若某事件機率為p，現重複試驗n次，該事件發生k次的機率為：P=C(n,k)×p^k×(1-p)^(n-k).C(n,k)表示組合數，即從n個事物中拿出k個的方法數。
套用條件
二項分布與常態分配2．已知發生某一結果（陽性）的機率為π，其對立結果的機率為1-π，實際工作中要求π是從大量觀察中獲得比較穩定的數值。
3．n次試驗在相同條件下進行，且各個觀察單位的觀察結果相互獨立，即每個觀察單位的觀察結果不會影響到其他觀察單位的結果。如要求疾病無傳染性、無家族性等。
性質
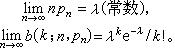二項分布公式μ=nπ（7.3）
σ=（7.4）
若均數和標準差不用絕對數表示，而是用率表示時，即對式（7.
3）和（7.4）分別除以n，得
μp=π（7.5）
σp=（7.6）
σp是樣本率的標準誤的理論值，當π未知時，常用樣本率p作為π的估計值，式（7.6）變為：
sp=（7.7）
2．二項分布的累計機率（cumulativeprobability）常用的有左側累計和右側累計兩種方法。從陽性率為π的總體中隨機抽取含量為n的樣本，則
（1）最多有k例陽性的機率
(7.8)
（2）最少有k例陽性的機率
（7.9）
其中，X=0,1,2,…，k,…，n。
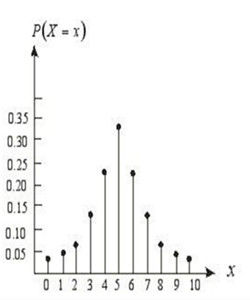
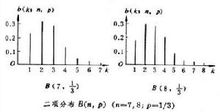
3．二項分布的圖形已知π和n，就能按公式計算X=0，1，…，n時的P（X）值。以X為橫坐標，以P（X）為縱坐標作圖，即可繪出二項分布的圖形，如圖7.1，給出了p=0.5和p=0.3時不同n值對應的二項分布圖。
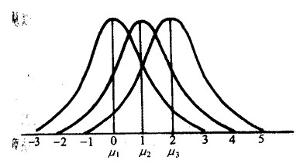
二項分布的形狀取決於π和n的大小，高峰在m=np處。當p接近0.5時，圖形是對稱的；p離0.5愈遠，對稱性愈差，但隨著n的增大，分布趨於對稱。當n→∞時，只要p不太靠近0或1，特別是當nP和n(1－P)都大於5時，二項分布近似於常態分配。關於二項分布近似為常態分配的判定條件，不同著述中存在爭議，在甘怡群《心理與行為科學統計》中：當np>10且n（1-p）>10時，二項分布可以近似為常態分配（第72頁）；在張厚粲《現代心理與教育統計學》中：當p（1-p）且n（1-p）≥5時，二項分布可以近似為常態分配（第178頁）。
π=0.5時,不同n值對應的二項分布
π=0.3時，不同n值對應的二項分布
分布區別
兩點分布又稱伯努利分布兩點分布的分布列就是
| x | 0 | 1 |
| P | 1-p | p |
列一個二項分布的分布列就是
X012………n
PC(0)(n)·(1-p)^nC(1)(n)·p·(1-p)^(n-1)……C(n)(n)·p^n·(1-p)^0
也就是說當n=1時，這個特殊二項分布就會變成兩點分布,
即兩點分布是一種特殊的二項分布
像其他地方說的二項分布是兩點分布的多重實驗也不無道理，因為兩者都是獨立的重複實驗,只不過次數不同罷了
E(n)=np
var(n)=np(1-p)(n是實驗次數，p是每次實驗的機率）
