角元塞瓦定理

角元塞瓦定理：設P為平面上一點（不在AB、BC、AC三條直線上），延長AP、BP、CP分別交對邊或其延長線於D、E、F三點，那么（sinBAP/sinPAC）（sinACP/sinPCB）（sinCBP/sinPBA）=1。

基本信息

• 英文名：角元塞瓦定理

• 提出時間：1687年
• 提出者：塞瓦
• 套用學科：平面幾何

簡介

角元塞瓦定理

在數學競賽中，證明平面幾何中的三線共點問題時，首選的方法是同一法，行之有效的方法是同一法，用得最多的方法還是同一法．近幾年來，同一法的老大地位已逐漸讓位於塞瓦定理的逆定理，其中當然包括角元塞瓦定理的逆定理．下面給出角元塞瓦定理的逆定理及其推論的證明。

逆定理

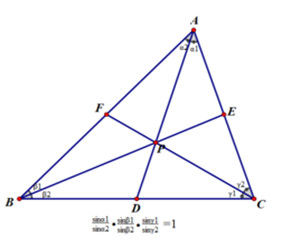
在三角形ABC三邊BC、AC、AB上分別取D、E、F三點，連線AD、BE，設它們交於P，連線CP、PF若(sinBAP/sinPAC)(sinACP/sinPCB)(sinCBP/sinPBA)=1，C、P、F在同一直線上，既AD、BE、CF三線共點．

內容

設P為平面上一點（不在AB、BC、AC三條直線上），且(sinBAP/sinPAC)(sinACP/sinPCB)(sinCBP/sinPBA)=1則AD、BE、CF三線共點或互相平行．

證明

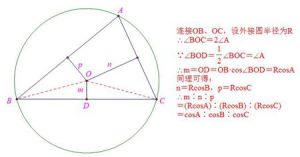
先證原定理，過P作PX⊥BA，PY⊥AC，PZ⊥CB，則sinBAP/sinPAC=PX：PY，sinACP/sinPCB=PY：PZ，sinCBP/sinPBA=PZ：PX，故乘積為1。逆定理可用同一法證明。

推論

若所引的三條線段都在△ABC內部，則這三條直線共點．

數學意義

數學競賽的教練和優秀選手經常用塞瓦定理的逆定理來證明三線共點問題，並不是因為人們對此定理有所偏愛，而是因為它好用且適用，比同一法更加行之有效．加之使用角元塞瓦定理時，不但可以與平面幾何中的許多定理配合套用，而且可以自然而然使用各種三角公式，因此，角元塞瓦定理的逆定理備受青睞．儘管這一逆定理的結論是“三線共點或互相平行”，但“三線互相平行”這一情形在大多數情況下都容易排除，並不影響用來證明三線共點問題．
此外，梅涅勞斯定理也可以協助塞瓦定理進行三點共線的證明，兩者經常結合使用。