歐拉線概述
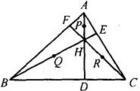 歐拉線
歐拉線歐拉於1765年在它的著作《三角形的幾何學》中首次提出定理:三角形的重心在歐拉線上,即三角形的重心、垂心和外心共線。
歐拉線的證明
作△ABC的外接圓,連結並延長BO,交外接圓於點D。連結AD、CD、AH、CH、OH。作中線AM,設AM交OH於點G’。 ∵ BD是直徑, ∴ ∠BAD、∠BCD是直角。 ∴ AD⊥AB,DC⊥BC。 ∵ CH⊥AB,AH⊥BC, ∴ DA∥CH,DC∥AH。 ∴ 四邊形ADCH是平行四邊形, ∴ AH=DC。 ∵ M是BC的中點,O是BD的中點。 ∴ OM= DC。 ∴ OM= AH。 ∵ OM∥AH, ∴ △OMG’ ∽△HAG’。 ∴ 。 ∴ G’是△ABC的重心。 ∴ G與G’重合。 ∴ O、G、H三點在同一條直線上。
歐拉線另證
設H,G,O,分別為△ABC的垂心、重心、外心。連線AG並延長交BC於D, 則可知D為BC中點。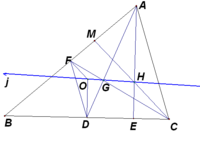
連線OD ,又因為O為外心,所以OD⊥BC。連線AH並延長交BC於E,因H為垂心,所以 AE⊥BC。所以OD//AE,有∠ODA=∠EAD。由於G為重心,則GA:GD=2:1。
連線CG並延長交BA於F,則可知D為BC中點。同理,OF//CM.所以有∠OFC=∠MCF
連線FD,有FD平行AC,且有DF:AC=1:2。FD平行AC,所以∠DFC=∠FCA,∠FDA=∠CAD,又∠OFC=∠MCF,∠ODA=∠EAD,相減可得∠OFD=∠HCA,∠ODF=∠EAC,所以有△OFD∽△HCA,所以OD:HA=DF:AC=1:2;又GA:GD=2:1所以OD:HA=GA:GD=2:1
又∠ODA=∠EAD,所以△OGD∽△HGA。所以∠OGD=∠AGH,又連線AG並延長,所以∠AGH+∠DGH=180°,所以∠OGD+∠DGH=180°。即O、G、H三點共線。
