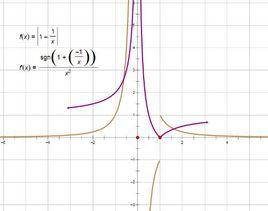
定義
如果函式f(x)在(a,b)中每一點處都可導,則稱f(x)在(a,b)上可導,則可建立f(x)的導函式,簡稱導數,記為f'(x)
如果f(x)在(a,b)內可導,且在區間端點a處的右導數和端點b處的左導數都存在,則稱f(x)在閉區間[a,b]上可導,f'(x)為區間[a,b]上的導函式,簡稱導數 。
若將一點擴展成函式f(x)在其定義域包含的某開區間I內每一個點,那么函式f(x)在開區間內可導,這時對於內每一個確定的值,都對應著f(x)的一個確定的導數,如此一來每一個導數就構成了一個新的函式,這個函式稱作原函式f(x)的導函式,記作:y'或者f′(x)。
函式f(x)在它的每一個可導點x。處都對應著一個唯一確定的數值——導數值f′(x),這個對應關係給出了一個定義在f(x)全體可導點的集合上的新函式,稱為函式f(x)的導函式,記為f′(x)。
導函式的定義表達式為:
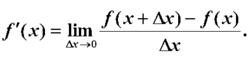 導函式
導函式值得注意的是,導數是一個數,是指函式f(x)在點x0處導函式的函式值。但通常也可以說導函式為導數,其區別僅在於一個點還是連續的點。
分類
基本函式的導函式
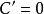 導函式
導函式其中C為常數
 導函式
導函式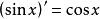 導函式
導函式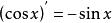 導函式
導函式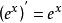 導函式
導函式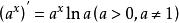 導函式
導函式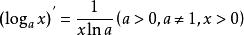 導函式
導函式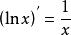 導函式
導函式和差積商函式的導函式
[f(x) + g(x)]' = f'(x) + g'(x)
[f(x) - g(x)]' = f'(x) - g'(x)
[f(x)g(x)]' = f'(x)g(x) + f(x)g'(x)
[f(x)/g(x)]' = [f'(x)g(x) - f(x)g'(x)] / [g(x)^2]
複合函式的導函式
設 y=u(t) ,t=v(x),則 y'(x) = u'(t)v'(x) = u'[v(x)] v'(x)
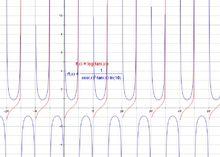 複合函式與其導函式
複合函式與其導函式例 :y = t^2 ,t = sinx ,則y'(x) = 2t * cosx = 2sinx*cosx = sin2x
條件
如果一個函式的定義域為全體實數,即函式在上都有定義,那么該函式是不是在定義域上處處可導呢?答案是否定的。 函式在定義域中一點可導需要一定的條件是:函式在該點的左右兩側導數都存在且相等。這實際上是按照極限存在的一個充要條件(極限存在它的左右極限存在且相等)推導而來。
例如:f(x)=|x|在x=0處雖連續,但不可導(左導數-1,右導數1)
 導函式
導函式上式中,後兩個式子可以定義為函式在處的左右導數:
| 左導數:f(x-)=-1 |
| 右導數:f(x-)=1 |
單調性
一般地,設函式y=f(x)在某個區間內有導數,如果在這個區間y'>0,那么函式y=f(x)在這個區間上為增函式:如果在這個區間y'<0,那么函式y=f(x)在這個區間上為減函式;如果在這個區間y'=0,那么函式y=f(x)在這個區間上為常數函式
導數極值
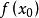 導函式
導函式 導函式
導函式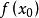 導函式
導函式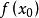 導函式
導函式 導函式
導函式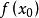 導函式
導函式一般地,設函式y=f(x)在x=x0及其附近有定義,如果的值比附近所有各點的函式值都大,我們說是函式y=f(x)的一個極大值;如果的值比附近所有各點的函式值都小,我們說是函式y=f(x)的一個極小值。極大值與極小值統稱極值。
在定義中,取得極值的點稱為極值點,極值點是自變數的值,極值指的是函式值。請注意以下幾點:
1.極值是一個局部概念。由定義,極值只是某個點的函式值與它附近點的函式值比較是最大或最小,並不意味著它在函式的整個的定義域內最大或最小。
2.函式的極值不是唯一的。即一個函式在某區間上或定義域內極大值或極小值可以不止一個。
3.極大值與極小值之間無確定的大小關係。即一個函式的極大值未必大於極小值。
4.函式的極值點一定出現在區間的內部,區間的端點不能成為極值點。而使函式取得最大值、最小值的點可能在區間的內部,也可能在區間的端點。
 導函式
導函式 導函式
導函式 導函式
導函式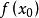 導函式
導函式 導函式
導函式 導函式
導函式 導函式
導函式 導函式
導函式5.在函式取得極值處,如果曲線有切線的話,則切線是水平的,從而有 f'(x) =0。但反過來不一定。如函式y=x3,在x=0處,曲線的切線是水平的,但這點的函式值既不比它附近的點的函式值大,也不比它附近的點的函式值小。 若滿足 =0,且在的兩側f(x)的導數異號,則是f(x)的極值點,是極值,並且如果 在x0兩側滿足“左正右負”,則是f(x)的極大值點,f()是極大值;如果 在x0兩側滿足“左負右正”,則是f(x)的極小值點,f()是極小值。
6.極值與最值的區別:極值是在局部對函式進行比較,最值是在整體區間上對函式值進行比較