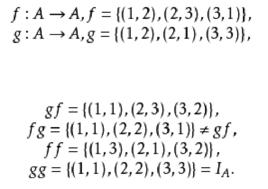定義
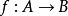 關於函式的複合運算
關於函式的複合運算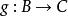 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算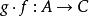 關於函式的複合運算
關於函式的複合運算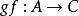 關於函式的複合運算
關於函式的複合運算設有定義在由集合A到集合B的函式 和定義在集合B到集合C上的函式 ,則 和 的複合函式是一個由集合A到集合C的函式,記為 (或記為 )。
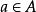 關於函式的複合運算
關於函式的複合運算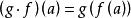 關於函式的複合運算
關於函式的複合運算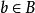 關於函式的複合運算
關於函式的複合運算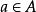 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算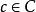 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算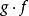 關於函式的複合運算
關於函式的複合運算對於任意一個元素 ,有 ,也就是說,如果 是 在函式 作用下的像,並且 是元素b在函式 作用下的像,那么集合C中的元素c就是 在複合函式 作用下的像 。
複合函式的定義域與值域
 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算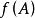 關於函式的複合運算
關於函式的複合運算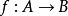 關於函式的複合運算
關於函式的複合運算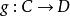 關於函式的複合運算
關於函式的複合運算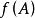 關於函式的複合運算
關於函式的複合運算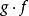 關於函式的複合運算
關於函式的複合運算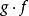 關於函式的複合運算
關於函式的複合運算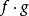 關於函式的複合運算
關於函式的複合運算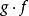 關於函式的複合運算
關於函式的複合運算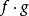 關於函式的複合運算
關於函式的複合運算在上述複合函式的定義中,要求函式 的值域包與函式g的定義域相等。實際上,對該條件可以適當放寬,即只要求函式 的值域 是函式g的定義域的子集就可以了。也就是說.若有函式 和函式 ,並且有f(A)是集合C的子集,則同樣可以定義一個由集合A到集合D的複合函式g·f。但是,如果 不是集合C的子集,那么,複合函式 就沒有意義了。因此,在上述定義的條件下,儘管複合函式 有意義,但是 不一定有意義,即使 與 都有意義,二者也不一定相等。
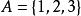 關於函式的複合運算
關於函式的複合運算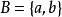 關於函式的複合運算
關於函式的複合運算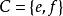 關於函式的複合運算
關於函式的複合運算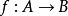 關於函式的複合運算
關於函式的複合運算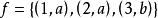 關於函式的複合運算
關於函式的複合運算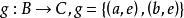 關於函式的複合運算
關於函式的複合運算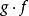 關於函式的複合運算
關於函式的複合運算例1 設集合 ,集合 ,集合 ,定義在集合A到集合B上的函式 , ,定義在集合B到集合C上的函式 ,求複合函式 。
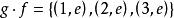 關於函式的複合運算
關於函式的複合運算根據複合函式的定義不難求出
 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算例2設集合 ,並且在由集合A到A自身上定義兩個函式 和函式 :
 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算求複合函式 。
解:根據複合函式的定義有:
 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算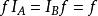 關於函式的複合運算
關於函式的複合運算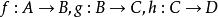 關於函式的複合運算
關於函式的複合運算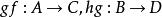 關於函式的複合運算
關於函式的複合運算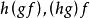 關於函式的複合運算
關於函式的複合運算由於函式的複合運算是關係的複合運算的一種特殊情形,因此關係的複合運算中成立的性質,對於函式的複合運算也是成立的。例如,對於任意一個函式,有。又例如,設有三個函式,根據定義不難看出,這些函式可以構成複合函式,進而可以構成複合函式,可以看出,這兩個複合函式都是由集合A到集合D的函式。又由於關係的複合運算滿足結合律,因此,函式的複合運算也滿足結合律,因此,可以得出以下定理 。
相關定理
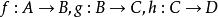 關於函式的複合運算
關於函式的複合運算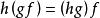 關於函式的複合運算
關於函式的複合運算定理1 設對於任意給定的三個函式 ,則有 。
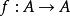 關於函式的複合運算
關於函式的複合運算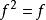 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算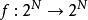 關於函式的複合運算
關於函式的複合運算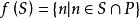 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算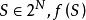 關於函式的複合運算
關於函式的複合運算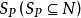 關於函式的複合運算
關於函式的複合運算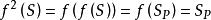 關於函式的複合運算
關於函式的複合運算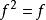 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算定義 設有定義在集合A到A自身的函式 ,且 ,則稱函式 為 冪等函式。例如,定義在正整數集的冪集上的函式 ,將其定義為 ,則根據函式 的定義,對於任意一個 為S中所有的素數組成的集合,記為 。而又由於 ,所以 ,因此這裡定義的函式 是一個冪等函式。
 關於函式的複合運算
關於函式的複合運算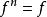 關於函式的複合運算
關於函式的複合運算如果函式 是冪等函式,那么對於所有的正整數n≥1,都有 。
 關於函式的複合運算
關於函式的複合運算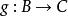 關於函式的複合運算
關於函式的複合運算定理 設有函式 和函式 ,那么:
 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算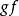 關於函式的複合運算
關於函式的複合運算(1) 如果 和 都是單射函式,則複合函式 也是單射函式;
 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算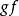 關於函式的複合運算
關於函式的複合運算(2) 如果 和 都是滿射函式,則複合函式 也是滿射函式;
 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算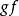 關於函式的複合運算
關於函式的複合運算(3) 如果 和 都是雙射函式,則複合函式 也是雙射函式。
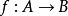 關於函式的複合運算
關於函式的複合運算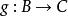 關於函式的複合運算
關於函式的複合運算定理 設有函式 和函式 ,那么:
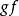 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算(1) 如果複合函式 是單射函式,則函式 是單射函式;
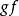 關於函式的複合運算
關於函式的複合運算(2) 如果複合函式 是滿射函式,則函式g是滿射函式;
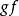 關於函式的複合運算
關於函式的複合運算 關於函式的複合運算
關於函式的複合運算(3) 如果複合函式 是雙射函式,則函式 是雙射函式,函式g是滿射函式 。