定義
若兩角之和滿足180°+2kπ(k∈Z),那么這兩個角 互為補角.其中一個角叫做另一個角的補角 。
備註:兩個角的所在位置並不影響其互為補角,要判斷兩個角是否互補,只需滿足: 兩個角的和等於180°+360°k,k∈Z。
性質
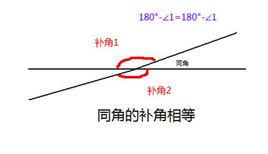
補角的性質: 同角或等角的補角相等。
它包括以下兩方面的內容:
1.同角的補角相等。即:若∠A+∠B=180°,∠A+∠C=180°,則∠C=∠B
2.等角的補角相等。即:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D,則∠C=∠B
區別
補角與餘角的區別
1、定義不同
如果兩個角的和是一個平角,那么這兩個角互為補角.其中一個角叫做另一個角的補角 。
∠A +∠C=180°即:∠C的補角=180°-∠C; ∠A的補角=180°-∠A
如果兩個角的和是一個直角,那么稱這兩個角互為餘角,簡稱互余。其中一個角是另一個角的餘角。
∠A +∠C=90°即:∠C的餘角=90°-∠C ;∠A的餘角=90°-∠A
2、計算方法不同
補角:180度減去這個角的度數。
餘角:90度減去這個角的度數。
餘角必由兩個銳角組成,互補的兩角,必有其一為鈍角或直角。 。
鄰補角
定義
兩個角有一條公共邊,它們的另一條邊互為反向延長線。具有這種關係的兩個角,互為鄰補角。補角只注重數量關係兩角之和是180°,即無論是否有公共邊均可,但鄰補角還要注重位置上的關係)。
性質
一個角與它的鄰補角的和等於180°。
如果兩個角互為鄰補角,那么它們的角平分線互相垂直。
特徵
1.具有一個公共的頂點;
2.有一條公共邊;
3.兩個角的另一邊互為反向延長線。
4.鄰補角是成對出現的,而且是互為鄰補角。
5.互為鄰補角的兩角相拼為平角。
6.互為鄰補角的兩角互補,即相加為180度。