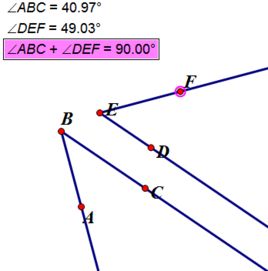
餘角性質
1. 同角或等角的餘角相等
若∠A+∠B=90°,∠D+∠C=90°,∠A=∠D
則有∠C=∠B。即得等角的餘角相等。
2.關於餘角的三角函式結論:
若 ∠A+∠B=90°,則有sinA=cosB,cosA=sinB;tanA×tanB=1。
餘角的習題
如圖,O是直線AB上的一點,OC平分∠AOB,∠DOE=90o,則(1)∠2=∠( 4 ),∠1=∠( 3 ) (2)圖中,互為餘角的角共有哪幾對? ( ∠1與∠2,∠1與∠4,∠2與∠3,∠4與∠3)
(3)圖中,∠DOB的補角是 ∠1,∠3。
解: ∠COF=∠ BOD
理由: ∵ ∠COF+∠ 3=1800 ∠ BOD+∠1=1800
又 ∵∠ 1 = ∠3
∴ ∠COF=∠ BOD