羅伯遜-沃爾克度規
正文
按照宇宙學原理在宇宙學尺度上天體系統最重要的特徵之一是均勻性和各向同性。H.P.羅伯遜和沃爾克分別於1935年和1936年證明,適應於上述均勻性和各向同性要求的四維時空只有三種,它們的時空度規具有下列形式: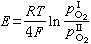 ,
,
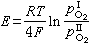
按照宇宙學原理在宇宙學尺度上天體系統最重要的特徵之一是均勻性和各向同性。
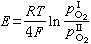 ,
,
簡介根據大爆炸理論,宇宙是由一個極緊密、極熾熱的奇點膨脹到現在的狀態。宇宙大爆炸(簡稱大爆炸)是描述宇宙誕生初始條件及其後續演化...
簡介 發展 理論概述 觀測證據 特點、疑點和問題的巨大成功。2宇宙學原理與羅伯遜-沃爾克度規1宇宙學原理現代宇宙學是建立在...觀測和宇宙微波背景輻射的高度各向同性所支持。2羅伯遜-沃爾克度規滿足宇宙學...φ^2}這一度規被稱為羅伯遜-沃爾克度規。其中r,φ,θ為共動坐標,r...
概念介紹黑洞愛因斯坦的廣義相對論理論在天體物理學中有著非常重要的套用:它直接推導出某些大質量恆星會終結為一個黑洞——時空中的某些...
概念介紹 誕生背景 基本假設 原理 理論內容,這個解後來被稱為弗里德曼-勒梅特-羅伯遜-沃爾克度規,並由此指出宇宙是膨脹...下落度規。這個度規是勒梅特宇宙模型的基礎。其後羅伯遜與沃克發展了勒梅特度規,得到更高維度(三維)對稱的羅伯遜-沃克度規,作為伽莫夫提出的大爆炸...
簡介 生平 人物貢獻 相關事件 大爆炸理論宇宙半徑 正文在均勻各向同性的宇宙模型中,有羅伯遜-沃爾克度規: 式中k為空間曲率署符,對於橢圓空間、歐氏空間和雙曲空間,分別為+1、0和...;因為這時我們可以把羅伯遜-沃爾克度規的空間部分當作四維歐氏空間中半徑為R...
宇宙半徑 正文 配圖 相關連線在1922年得出[1],他通過在弗里德曼-勒梅特-羅伯遜-沃爾克度規下對具有...概述 這個假設要求宇宙的度規具有如下形式:(圖一) 弗里德曼方程(英文...大於一億秒差距的尺度上是合理的。這個假設要求宇宙的度規具有如下形式...
概述 方程弗里德曼方程而提出,這個解後來被稱作弗里德曼-勒梅特-羅伯遜-沃爾克度規...觀測到的宇宙中輕元素的豐度,和理論所預言的宇宙早期快速膨脹並冷卻過程中最初的幾分鐘內,通過核反應所形成的這些元素的理論豐度值非常接近,定性並定量...
定義和起源 動機和發展 驗證直覺 大爆炸年表 特點、疑點和問題可以推導出演化態宇宙的羅伯遜-沃爾克度規。運用完全宇宙學原理則能得到穩恆態宇宙度規,利用不同的度規可建立各種宇宙模型。宇宙存在原理 宇宙存在原理由...
詳細內容 宇宙存在原理可以推導出演化態宇宙學的羅伯遜-沃爾克度規。運用完全宇宙學原理則能得到穩恆態宇宙學度規,利用不同的度規可建立各種宇宙模型。 相關條目...
基本概念 相關條目