弗里德曼方程

弗里德曼方程 是廣義相對論框架下描述空間上均一且各向同性的膨脹宇宙模型的一組方程。

簡介

他通過在弗里德曼-勒梅特-羅伯遜-沃爾克度規下對具有給定質量密度和壓力的流體的能量-動量張量套用愛因斯坦引力場方程而得到。而具有負的空間曲率的方程則由弗里德曼在1924年得到。

假設

參見：弗里德曼-勒梅特-羅伯遜-沃爾克度規弗里德曼方程所基於的假設是宇宙在空間上是均一且各向同性的；從今天的經驗來看，這個假設在大於一億秒差距的尺度上是合理的。這個假設要求宇宙的度規具有如下形式：

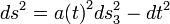弗里德曼方程

其中宇宙標度因子

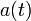弗里德曼方程

只與時間有關，因

而三維空間度規

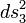弗里德曼方程

必須是下面三種形式之一：

平直空間（曲率處處為零）

具有常數正曲率的三維球面

具有常數負曲率的三維雙曲面

在下面的討論中，這三種情形各自對應著一個參數k的值，分別為0，1，-1。而

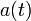弗里德曼方程

被稱作宇宙標度因子，它能夠通過愛因斯坦場方程和宇宙間物質的能量和應力聯繫。