算圖
正文
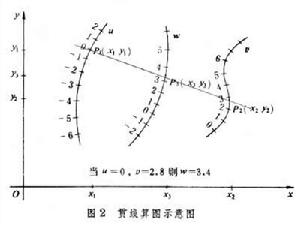
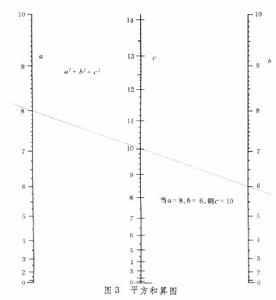
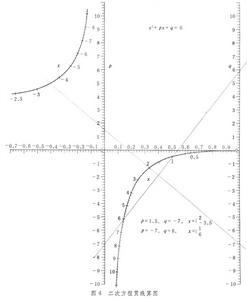
又稱諾模圖,系指根據一定函式關係式由若干有刻度的線條所構成的特定圖形,可用來進行計算。例如,根據指數函式關係式ω=uυ可制出算圖如圖1。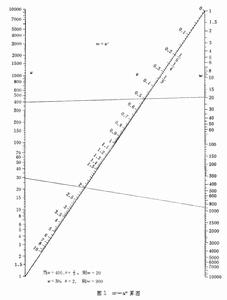 若變元u、υ的值已知,則在圖中u,υ軸上定兩點,作一直線,即能求得未知變元ω 的值。由於算式的函式關係都隱含於算圖的線條和刻度之中,而圖上只顯出各變元的數值,因此計算操作極為方便,不要求使用者先經任何訓練或具備其他用具。計算精度雖受圖形限制,只達有效數字三位上下,但一般已可滿足實際需要。在科學技術各部門,算圖都有廣泛套用。
若變元u、υ的值已知,則在圖中u,υ軸上定兩點,作一直線,即能求得未知變元ω 的值。由於算式的函式關係都隱含於算圖的線條和刻度之中,而圖上只顯出各變元的數值,因此計算操作極為方便,不要求使用者先經任何訓練或具備其他用具。計算精度雖受圖形限制,只達有效數字三位上下,但一般已可滿足實際需要。在科學技術各部門,算圖都有廣泛套用。 算圖分為貫線算圖和網路算圖兩類。
貫線算圖 又名列線圖。它的基本要求為三點共線。設三點及其坐標為p1(x1,y1)、p2(x2,y2)、p3(x3,y3),則p1、p2、p3共線的充要條件為
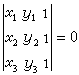 。 (1)
。 (1)
F(u,υ,ω)=0, (2)
設此式可化為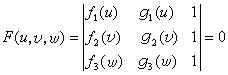 , (3)
, (3)
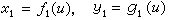 ; (4)
; (4) 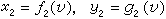 ; (5)
; (5) 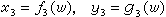 。 (6)在(4)中,以變元u作為參數,可得出點p1(x1,y1)的軌跡,稱為u尺度(簡稱u尺),(4)稱為u尺的尺度方程。同樣,(5)、(6)分別為υ尺、ω尺的尺度方程。用此三組尺度方程即可繪製u、υ、ω三尺度,構成貫線算圖。
。 (6)在(4)中,以變元u作為參數,可得出點p1(x1,y1)的軌跡,稱為u尺度(簡稱u尺),(4)稱為u尺的尺度方程。同樣,(5)、(6)分別為υ尺、ω尺的尺度方程。用此三組尺度方程即可繪製u、υ、ω三尺度,構成貫線算圖。
圖1的繪製方法是將原有算式ω=uυ化為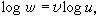 故
故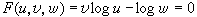 。為使此算式化為行列式,試引入輔助參數s、t,使s=logu,t=logω,並代入上式而得三聯立式關於s、t、1的齊次線性方程組
。為使此算式化為行列式,試引入輔助參數s、t,使s=logu,t=logω,並代入上式而得三聯立式關於s、t、1的齊次線性方程組
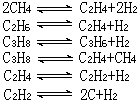 。
。
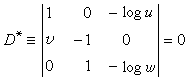 ,
,
 化為(3)的形式,可得
化為(3)的形式,可得 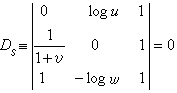 。
。
 稱初始行列式;Ds稱標準行列式。二者都可還原為算式F(u,υ,ω)=0。
稱初始行列式;Ds稱標準行列式。二者都可還原為算式F(u,υ,ω)=0。 從(4)、(5)、(6)可得關於ω=uυ算圖的三組尺度方程:
u尺 x1=0,y1=logu(u尺在y軸上,用對數刻度);
υ尺
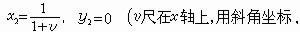
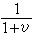

ω尺 x3=1,y3=-logω (ω尺平行y軸, 距y軸單位長,用反向對數刻度)。
若三元函式F(u,υ,ω)=0取函式乘法關係
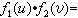 ƒ3(ω)的形式(縮記為ƒ1ƒ2=ƒ3),可得D
ƒ3(ω)的形式(縮記為ƒ1ƒ2=ƒ3),可得D 及Ds為
及Ds為 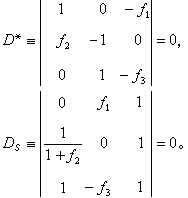
 算圖
算圖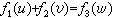 即
即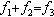 的形式,依上法可得D
的形式,依上法可得D 及Ds為
及Ds為 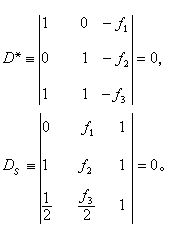
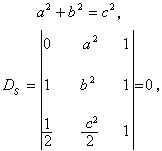 (7)
(7)
 )。此種算圖由三平行尺度構成,故稱為三平算圖,在算圖中套用最廣。例如,對算式ƒ1ƒ2=ƒ3,經取對數後,可化成logƒ1+logƒ2=logƒ3。又如,uυ=ω 也可用重對數化成loglogu+logυ=loglogω,從而都可以作出三平算圖。
)。此種算圖由三平行尺度構成,故稱為三平算圖,在算圖中套用最廣。例如,對算式ƒ1ƒ2=ƒ3,經取對數後,可化成logƒ1+logƒ2=logƒ3。又如,uυ=ω 也可用重對數化成loglogu+logυ=loglogω,從而都可以作出三平算圖。 有的三元算式 F(u,υ,ω)=0中有兩個含某一變元的不同函式,一般形式為:
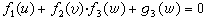
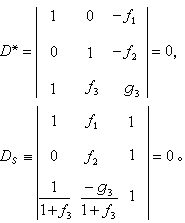
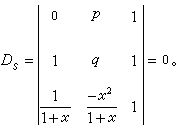
 算圖
算圖 及Ds,以求得u、υ、ω三尺的尺度方程。除此法以外,亦可不用行列式,只將F=0按其類型,諸如ƒ1+ƒ2=ƒ3,ƒ1ƒ2=ƒ3,ƒ1+ƒ2ƒ3+g3=0等各種形式,選定三平算圖,Z形算圖、平曲算圖等貫線算圖格式,然後作出尺度方程。後一方法易為初學者掌握。
及Ds,以求得u、υ、ω三尺的尺度方程。除此法以外,亦可不用行列式,只將F=0按其類型,諸如ƒ1+ƒ2=ƒ3,ƒ1ƒ2=ƒ3,ƒ1+ƒ2ƒ3+g3=0等各種形式,選定三平算圖,Z形算圖、平曲算圖等貫線算圖格式,然後作出尺度方程。後一方法易為初學者掌握。 網路算圖 它的基本要求是三線共點。同貫線算圖的三點共線形成幾何學的對偶關係。對於給定算式F(u,υ,ω)=0,網路算圖的適用範圍比貫線算圖更為廣泛,但其使用和製作比貫線算圖困難,精度也低。因此,網路算圖只成為算圖中次要類型,或與主要類型貫線算圖配合使用。
下面以二次方程 t2+pt+q=0為例繪製網路算圖。在此,算式F(p,q,t)=0,用直角坐標,使p=x, q=y而形成p族直線和q族直線(即縱橫坐標網)。當t取0,±1,±2等值,可得q=0, ±p+q+1=0, ±2p+q+4=0 等直線,形成t族直線。當p、q取定值,此p線和q線交點所經過的t線有兩條,即可以讀出所求t的兩根(圖5
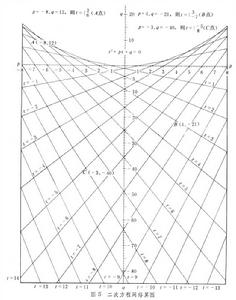 )。
)。 除三元算式以外,四元算式以及五元以上的算式,也都可作出算圖。對於四元算式F(u,υ,ω ,t)=0,在一定條件下可引入過渡變元R,將原式分解為兩個三元函式:
F1(u,υ,R)=0, F2(ω ,t,R)=0。
如算式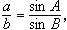
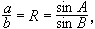
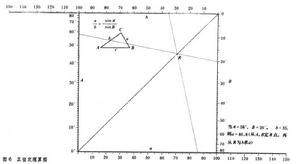 )。R尺為兩算圖的共同尺度,其上不用刻度點,只使第一貫線的交點決定第二貫線即可。這樣,
)。R尺為兩算圖的共同尺度,其上不用刻度點,只使第一貫線的交點決定第二貫線即可。這樣, sin B=b) sin A/α
或b)=α sin B/sin A
的值可以讀出。上述四元算式的分解法是由兩組貫線算圖利用共同尺度複合而成,故稱為複合算圖。也可由貫線算圖與網路算圖相結合或兩網路算圖相結合,甚至用三組複合算圖來處理更複雜的多元算式。
