大氣動力方程
正文
描寫大氣運動和狀態變化的方程。在大氣動力學中，根據經典力學的牛頓運動定律，特別是牛頓第二運動定律,推導出大氣運動方程；根據質量守恆定律,推導出大氣連續方程；根據熱力學第一定律得出熱流量方程；再加上狀態方程和水汽方程，就構成了描寫大氣運動和狀態變化（包括水的相變）的動力方程組。這套方程組是研究大氣的一切運動和現象的基礎。動 力 方 程 組
運動方程 在固定於地面的坐標中，對單位質量氣塊而言，由牛頓第二定律得大氣運動方程的矢量形式為
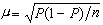
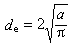為重力；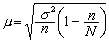
為氣壓梯度力（ρ、p分別為空氣的密度和氣壓）；ω為地球自轉角速度矢量，為科里奧利力；F為粘性力，主要是湍流粘性力（見大氣中的作用力）。 連續方程 大氣是具可壓縮性的連續介質，由質量守恆定律可得：
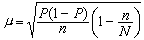
這就稱為連續方程。 式中墷·（pv）為三維質量散度。稱為三維速度散度,其中u、v、w分別是x、y、z方向的速度分量。為水平速度的散度，D>0，為水平輻散；D<0，為水平輻合。
熱流量方程 由熱力學第一定律可推出熱流量方程：
式中cp為定壓比熱,θ為位溫，Q為單位質量氣塊在單位時間內從外界得到的熱量,這屬於非絕熱加熱。通常Q =Q1+Q2+Q3，其中Q1為輻射加熱,Q2為潛熱加熱，Q3為感熱加熱（主要是湍流感熱輸送）。
在運動過程中,如果大氣不與外界交換熱量，即Q=0，則熱流量方程變為絕熱方程：
在絕熱過程中，氣塊的位溫守恆。位溫常用來識別氣團。
狀態方程 均勻物質系統處於熱力學平衡狀態時，其體積、壓強和溫度間的關係式。在對流層和平流層的大氣，可視為理想氣體,其氣壓<p、氣溫T 和密度ρ 遵守理想氣體狀態方程
式中R為摩爾氣體常數，Mr為空氣分子的相對質量，Rd為乾空氣氣體常數。
水汽方程 決定濕空氣氣塊中的水汽含量變化的方程：
式中q 為比濕（在一定容積的濕空氣中，水汽質量和濕空氣品質之比），S 為單位質量濕空氣在單位時間內從外界得到的水汽量。通常S =S1+S2, 其中S1、S2分別為相變和水汽擴散（主要是湍流擴散）造成的水汽變化。
上面五個方程構成了描寫大氣運動的基本方程組，這是由V.皮耶克尼斯於1904年首先建立的。其中任一物理量A 的個別變化dA/dt，都可以表示為 式中дA/дt為 A 的局地變化項；v·墷A 為平流項，它又可分為水平平流和鉛直平流兩個部分。平流變化代表某一氣塊的物理量A 在平流運動中不變時，它沿氣流方向移到某地（或某高度）之後，使該地同一物理量所產生的變化。
常 用 方 程
根據動力方程組，可以導出大氣動力學中幾個常用的方程。
渦度方程 速度場的鏇度，在氣象學中稱為渦度。
三維渦度方程 將運動方程作鏇度運算(即墷×),就得到地球大氣的三維渦度方程： 式中ωa=ωr+2ω,為氣塊的絕對渦度。2ω為牽連渦度，是由於大氣和地球一起鏇轉引起的；ωr= 墷×v=ξi +ηj+ζk ,為氣塊的相對渦度，其中i、j、k 為x、y、z方向的單位矢量,ξ、η、ζ分別為相對渦度在x、у、z方向上的分量： 鉛直渦度方程 研究大氣的大尺度運動（水平尺度ι)的量級為103公里）時，由於它是準水平的運動，在這種情況下，可以得到一個鉛直渦度方程，其形式為 式中x指向東，у 指向北，z 鉛直向上；f為科里奧利參數，ζ+f =ζa是絕對渦度的鉛直分量；Fx、Fy分別為粘性力在x、у方向的分量。鉛直渦度方程右端第一項為渦管項；第二項為力管項；第三項為摩擦項。
絕對渦度守恆 對於正壓（見正壓大氣）無摩擦運動，鉛直渦度方程化為
又無輻散運動，則：
這說明，在無摩擦的條件下，氣塊作正壓無輻散運動時，始終保持絕對渦度守恆。上式可以寫成：
式中，為羅斯比參數。
鉛直渦度ζ在天氣實踐中套用頗多，通常北半球氣鏇式流場，ζ>0；反氣鏇式流場，ζ<0（見大氣波動）。在地轉風的條件下，若用氣壓p 作鉛直坐標，則ζ可以用重力位勢Ф來表示（見大氣運動的平衡狀態）：
墷2p為等壓面上的拉普拉斯算符，ξg稱為地轉渦度。
位勢渦度方程 將運動方程、連續方程、熱流量方程結合在一起，得位勢渦度方程:
式中為位勢渦度。
位勢渦度守恆定律 對於絕熱無摩擦的大氣運動，Q =0，F =0，則有： 它稱為位勢渦度守恆定律，是H.埃特爾在1942年發現的。
對於大氣大尺度水平運動來說，在氣壓坐標中有： 因此位勢渦度守恆定律可改寫為 用這公式表達的位勢渦度守恆定律，是 C.-G.羅斯比在1940年發現的，它是大氣大尺度運動在絕熱、無摩擦和準地轉條件下的綜合定律。根據此定律，我們可以較方便地解釋非絕熱加熱的鉛直不均勻性對大氣穩定度的影響，以及南北向大地形在形成長波槽中的作用。
散度方程 對於大尺度運動，常用（水平）散度方程。它是由水平運動方程作水平散度運算而得，其形式為 式中是氣壓坐標系中的鉛直速度。
對於無摩擦的水平運動，散度方程化為 平衡方程 對於無摩擦、無輻散的水平大尺度運動，在氣壓坐標中，散度方程轉化為平衡方程： 式中所有對x和у的微商，都是指在氣壓坐標中的微商。因為它是在水平無輻散的條件下得到的，故可以引入流函式ψ: 這時，平衡方程又可表達為 平衡方程給出了風場和氣壓場之間更普遍的關係。地轉風的關係只是平衡方程在特定條件下的例子。對於分布均勻的圓形流線來說，在f為常數的情形下，平衡方程就表示了梯度風關係。
參考書目
J.PedloskyGeophysicalFluid Dynamics,Springer-Verlag，New York，1979.J.R.霍爾頓著，中國人民解放軍空軍氣象學院訓練部譯：《動力氣象學引論》，科學出版社，北京，1980。
J.R.Holton，AnIntroduction to Dynamic Meteoro-logy，2nd ed.，Academic Press，London，1979.
