和算

和算

正文

日本傳統數學。按狹義的理解，17世紀至19世紀中葉二百餘年間，是和算的興盛時期，和算即是專指這一時期(江戶時期)的日本數學。明治維新(1868)以後，由於西方數學不斷傳入，和算逐漸衰廢。
在和算發展的初期，曾受到中國古代數學的很大影響。至8世紀初,日本已仿照隋唐時期的數學教育制度設定算學博士並採用《周髀算經》、《九章算術》、《孫子算經》、《綴術》等中國古算書作為教材（見《算經十書》）。在流傳至今最早的和算書《口游》(970)中，還可以看到中國數學的影響。但是,直到15世紀之前,和算並沒有較大發展。
進入16世紀以後，伴隨著城市手工業和工商業的發展，對計算數學的要求日益迫切。中國元代數學家朱世傑所著《算學啟蒙》和明代數學家程大位所著《算法統宗》等先後傳入日本，對和算的前期發展產生了重大影響。1622年出版了現存最早的印刷本和算書《割算書》（毛利重能著）。1627年出版的《塵刼記》（吉田光由著），使珠算術在日本迅速得到普及。從內容上看《塵刼記》與《算法統宗》極為類似，但其中許多算題都是根據日本的實際情況而編寫的。此書在以後的二百餘年間，先後出版了各種不同版本達三百餘種，在日本廣為流行。早期的和算書還可以舉出《諸勘分物》（百川治兵衛）、《豎亥錄》（今村知商，1639）等。
從17世紀70年代開始，由於関孝和學派（関流）幾代人的努力，和算進入了興盛時期。関孝和在日本備受尊崇，被稱為算聖。関氏學派的主要成就是“點竄術”和“圓理”。“點竄術”把由中國傳入的天元術改為筆算並在算式的記法方面作了改進，是和算特有的筆算代數學。“圓理”是和算所特有的數學分析。經過不斷的發展，它在某些問題上取得了和西方微積分學相類似的若干成果。関孝和的弟子建部賢弘利用二分弧、四分弧等逐漸加倍分弧的方法求得關於弧長的無窮級數表達式，亦即相當於得出：

這是圓理的初期成果之一。除“點竄術”和“圓理”之外，在方程式論、行列式、幻方、連分數和不定方程解法等方面，関氏學派也作出了不少成果。屬於関氏學派的和算家還有中根元圭、久留島羲太、松永良弼、山路主任等人。山路的學生安島直円在計算圓面積時，曾先用一組平行線將圓割為許多極狹的矩形，再行求出這些矩形面積和的極限。這一思想擴大了圓理的套用範圍。橢圓以及其他平面曲線圍成的面積、弧長等等，皆可循此算出；進而曲面的表面積以及體積的求積等問題均可用無窮級數進行求解（相當於重積分）。晚期的関氏學派和算家和田寧進一步改進了圓理。他利用了微小的切線線段進行計算，製作了很多數表，使計算弧長、面積、體積等問題，更加簡化。他所用的方法和現代通用的積分法，在原理上十分接近。但是，用圓理可積分的函式還只限於是代數函式的若干特定類型。
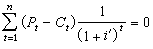
除関氏學派之外，還有一些較小的和算學派。值得注意的有會田安明與関氏學派間的抗衡。這種抗衡產生了不少數學著作。各學派之間這種相互競爭又對各自的算法相互保密的關係，頗與中世紀手工業行會的性質相似。
從16世紀開始，西方數學開始傳入日本；19世紀中葉日本採取開國政策之後，西方數學大量傳入。明治維新時期，在日本政府明令“和算廢止，洋算專用”之後，和算迅速衰廢。只有珠算仍被沿用至今。日本算盤，上一珠，下五珠，珠的截面呈菱形，運算時只用拇、食二指。
據統計，歷史上留有姓名的和算家約在 300人左右，著作約5000部。

配圖

相關連線