定義
一
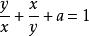 齊次方程
齊次方程1、所含各項關於未知數具有相同次數的方程,例如等。它們的左端,都是未知數的齊次函式或齊次多項式。2、右端為零的方程(組)亦稱為齊次方程(組),例如線性齊次(代數)方程組、齊次微分方程等。
二
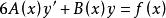 齊次方程
齊次方程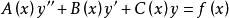 齊次方程
齊次方程 齊次方程
齊次方程1、線性方程乘積的導數。 或 等等為線性方程當 時稱為齊次方程。
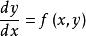 齊次方程
齊次方程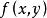 齊次方程
齊次方程 齊次方程
齊次方程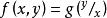 齊次方程
齊次方程2、如果一個一階微分方程 中的函式 可寫成 的函式,即 ,則這個方程是齊次方程。
釋義
“齊次”從詞面上解釋是“次數相等”的意思。
微分方程中有兩個地方用到“齊次”的叫法:
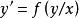 齊次方程
齊次方程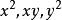 齊次方程
齊次方程 齊次方程
齊次方程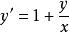 齊次方程
齊次方程1、形如 的方程稱為“齊次方程”,這裡是指方程中每一項關於x、y的次數都是相等的,例如 都算是二次項,而 算0次項,方程 中每一項都是0次項,所以是“齊次方程”。
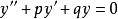 齊次方程
齊次方程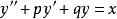 齊次方程
齊次方程2、形如 (其中p和q為關於x的函式)的方程稱為“齊次線性方程”,這裡“線性”是指方程中每一項關於未知函式y及其導數y',y'',……的次數都是相等的(都是一次),“齊次”是指方程中沒有自由項(不包含y及其導數的項),方程 就不是“齊次”的,因為方程右邊的項x不含y及y的導數,因而就要稱為“非齊次線性方程”。
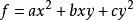 齊次方程
齊次方程另外線上性代數裡也有“齊次”的叫法,例如 稱為二次齊式,即二次齊次式的意思,因為f中每一項都是關於x、y的二次項。
形式
如果一階微分方程
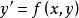 齊次方程
齊次方程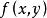 齊次方程
齊次方程 齊次方程
齊次方程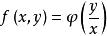 齊次方程
齊次方程中的函式 可寫成 的函式,即 ,則稱這方程為齊次方程。例如
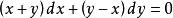 齊次方程
齊次方程是齊次方程,因為其可化為
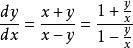 齊次方程
齊次方程特點解法
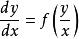 齊次方程
齊次方程(1)特點:方程中每一項的次方相同,且都可以化為一般形式 。
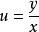 齊次方程
齊次方程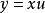 齊次方程
齊次方程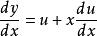 齊次方程
齊次方程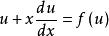 齊次方程
齊次方程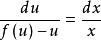 齊次方程
齊次方程 齊次方程
齊次方程 齊次方程
齊次方程(2)解法:令 ,即 ,則 ,於是原方程可化為 ,即 ,成為可分離變數的微分方程,求解後再用 代替 即得原方程的通解。
微分方程
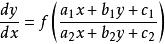 齊次方程
齊次方程形如方程
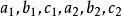 齊次方程
齊次方程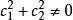 齊次方程
齊次方程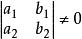 齊次方程
齊次方程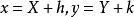 齊次方程
齊次方程其中 為常數,且 .當 時,令 ,由
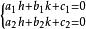 齊次方程
齊次方程解出h與k,可將原方程化為齊次方程
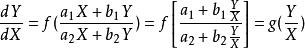 齊次方程
齊次方程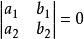 齊次方程
齊次方程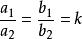 齊次方程
齊次方程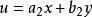 齊次方程
齊次方程當 時,即 ,可設 ,代入原方程後可化為可分離變數的微分方程,既有
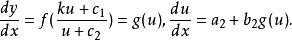 齊次方程
齊次方程
