基本介紹
稀疏集 設X為一距離空間,A是X的子集。如果A在X的任何一個非空開集中均不稠密,則稱A為 稀疏集。
定義中的非空開集可以換成非空開球,下面的定理給出稀疏集的一個特徵。
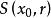 第一類型集
第一類型集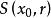 第一類型集
第一類型集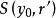 第一類型集
第一類型集定理1 距離空間X的子集A為稀疏集的充分必要條件是對任一開球,存在另一個含於中的開球使
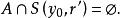 第一類型集
第一類型集定義 設A為距離空間X的子集,如果A可以表示成至多可列個稀疏集的並,則稱A是 第一類型集,又稱“ 第一綱集”,凡不是第一類型的集均稱為 第二類型集,又稱“ 第二綱集”。
因此,距離空間X的子集或者是第一類型的集或者是第二類型的集,二者必居其一。
有限個或可數個第一類型集的和是第一類型的集 。
例題分析
 第一類型集
第一類型集 第一類型集
第一類型集例1(1)n維Euclid空間中的任一有限子集是稀疏集,特別地,任一單元素集是稀疏集,因此中的任一可列集是第一類型的集。
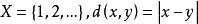 第一類型集
第一類型集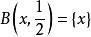 第一類型集
第一類型集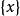 第一類型集
第一類型集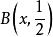 第一類型集
第一類型集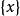 第一類型集
第一類型集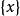 第一類型集
第一類型集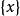 第一類型集
第一類型集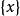 第一類型集
第一類型集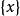 第一類型集
第一類型集(2)設,因為,故在中稠密,於是不是稀疏集。因此,包含在中的任一稀疏集必為空集。如果是可數個稀疏集的並,則必為空集,這樣就產生了矛盾。因此,為第二綱集。
第一類型的集與第二類型的集都是相對於一定的距離空間而言的,因而也都與事先給定的空間有著不可分割的聯繫 。
相關定理
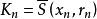 第一類型集
第一類型集定理2設X是完備的距離空間,是X中的一列閉球,滿足
 第一類型集
第一類型集(稱為閉集套).
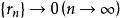 第一類型集
第一類型集 第一類型集
第一類型集如果,則有唯一的點含於所有球中。
定理2的逆命題也成立。
定理3 如果距離空間X中的任一半徑趨於零的閉球套都有非空的交,則空間X是完備的。
下面的定理給出了完備距離空間的一個重要特性。
定理4(貝爾(Baire))完備的距離空間是第二類型的集 。
