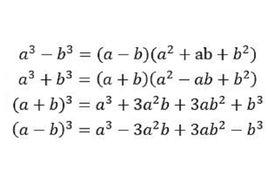簡介
立方差公式與立方和公式統稱為立方公式，兩者基本描述如下 ：
立方和公式，即兩數立方和等於這兩數的和與這兩數平方和與這兩數積的差的積。也可以說兩數立方和等於這兩數積與這兩數差的不完全平方的積 。
立方差公式，即兩數立方差等於這兩數差與這兩數平方和與這兩數積的和的積。也可以說，兩數立方差等於兩數差與這兩數和的不完全平方的積 。
證明
初級證明
由於立方項不好拆分，但是我們學過，遇到高階項要儘量採用低階項來對其進行簡化處理，所以很容易想到a ，同時由於對a 降階的同時還要和b 進行結合，所以很容易想到a b這樣一個加法項，因此對上式採取分別加和減一個a b項，得到下式，同時進行相應的合併
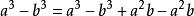立方差公式
立方差公式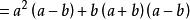
立方差公式
立方差公式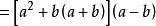證得：
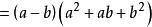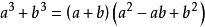立方差公式高級證明
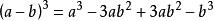立方差公式因為
所以根據交換律法則：
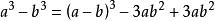立方差公式
立方差公式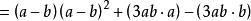
立方差公式
立方差公式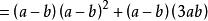
立方差公式 立方差公式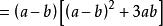證得：
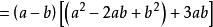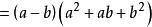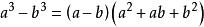立方差公式公式推廣
類似的，我們有立方和公式及其推廣：
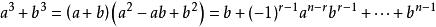立方差公式n為大於零的奇數，r為中括弧內項的序數，後面括弧中各項式的冪之和都為n-1，a 表示a的n次方。(n大於0且n不等於2)
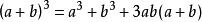立方差公式解題時常用它的變形：
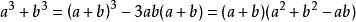立方差公式和
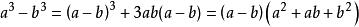立方差公式相應的，立方差公式也有變形
因此其推廣 ：
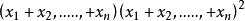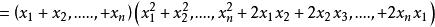立方差公式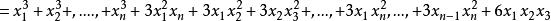
立方差公式
立方差公式