定義
一.如果數列{Xn},{Yn}及{Zn}滿足下列條件：
夾逼定理 夾逼定理（1）當n>時，其中∈N*，有Yn≤Xn≤Zn，
（2）{Yn}、{Zn}有相同的極限a，設-∞<a<+∞
則，數列{Xn}的極限存在，且當 n→+∞，limXn =a。
夾逼定理
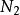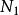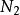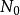夾逼定理 夾逼定理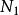 夾逼定理 夾逼定理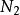 夾逼定理 夾逼定理證明：因為limYn=a，limZn=a，所以根據數列極限的定義，對於任意給定的正數ε，存在正整數、，當n>時 ，有〡Yn-a∣﹤ε，當n>時，有∣Zn-a∣﹤ε，取N=max{，，}，則當n>N時，∣Yn-a∣<ε、∣Zn-a∣<ε同時成立，且Yn≤Xn≤Zn，即a-ε<Yn<a+ε，a-ε<Zn<a+ε，又因為 a-ε<Yn≤Xn≤Zn<a+ε，即∣Xn-a∣<ε成立。也就是說
limXn=a
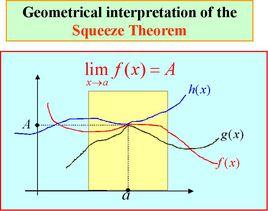
函式的夾逼定理二.
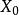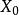夾逼定理 夾逼定理F(x)與G(x)在連續且存在相同的極限A，即x→時, limF(x)=limG(x)=A
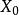夾逼定理則若有函式f(x)在的某鄰域內恆有
F(x)≤f(x)≤G(x)
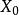夾逼定理則當X趨近,有limF(x)≤limf(x)≤limG(x)
即 A≤limf(x)≤A
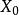夾逼定理故 limf()=A
簡單的說：函式A>B,函式B>C，函式A的極限是X，函式C的極限也是X ，那么函式B的極限就一定是X，這個就是夾逼定理。
套用
1.設{Xn}，{Zn}為收斂數列，且：當n趨於無窮大時，數列{Xn}，{Zn}的極限均為：a.
若存在N，使得當n>N時，都有Xn≤Yn≤Zn,則數列{Yn}收斂，且極限為a.
2.夾逼準則適用於求解無法直接用極限運算法則求極限的函式極限，間接通過求得F(x)和G(x)的極限來確定
f(x)的極限
