簡介
正二邊形（digon）是一個二位退化正多邊形，有兩個點和兩個邊。（在歐幾里德空間中，這兩個邊是重疊的，且它面積為0，但在球形空間中，邊就不一定重疊，且可以有面積）同時它也是半截正方形。
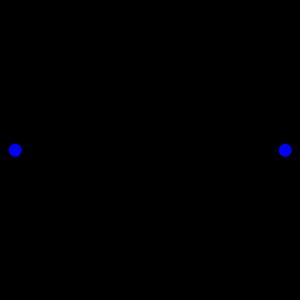歐式空間中的正二邊形
球形空間中的正二邊形特性
自身特性在歐式空間中，由於二邊形兩邊重疊，所以它必然是正的。同時，它不符合多邊形內角和定理所導出的外角定理（內角合定理還是符合的）。但在球形空間中就不一樣了，由於兩邊不一定重疊，二邊形也不一定是正的。
它也是半截正方形，與正四面體（三維）、正十六胞體（四維）同屬半截立方體（demihypercube）。
由於在歐式空間中，正二邊形和線段看起來一樣，自然就會有人想到用正二邊形代替多面體的線段，這就會使多面體的棱增加一倍，並且原來的棱都變成了面（雖然面積都為0），這種轉變並沒有對歐拉特徵產生影響（χ= V - E + F）。
