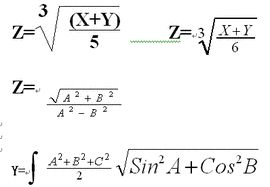公式
(a-b)³=a³-3a²b+3ab²-b³;注意:在(a-b)³=a³-3a²b+3ab²-b³中,按第一個字母排列後它的號是“+、-.+、-”,它是一個齊次式(每一項都是3次),它的係數是1、-3、+3、-1,結果是四項式。
分解
基本形式
(a-b)³=(a-b)(a-b)(a-b)=(a²-2ab+b²)(a-b)=a³-3a²b+3ab²-b³
過程
兩數差乘以它們的平方和與它們的積的和等於兩數的立方差。
(a-b)³=a³-3a²b+3ab²-b³
所以a³-b³=(a-b)³-[-3(a²)b+3ab²]=(a-b)(a-b)²+3ab(a-b)
=(a-b)(a²-2ab+b²+3ab)=(a-b)(a²+ab+b²:
(1) a³+b³=(a+b)(a²-ab+b²)
(2) a^n+b^n=(a+b)[a^(n-1)-a^(n-2)×b+...+(-1)^(r-1)×a^(n-r)×b^(r-1)+...+b^(n-1)](n為 奇數) (後面括弧中各項式的冪之和都為n-1)
a^n表示a的n次方