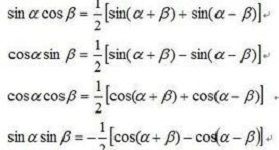計算公式
積化和差公式是由正弦或餘弦的和角公式與差角公式通過加減運算推導而得。sinαsinβ=-[cos(α+β)-cos(α-β)]/2
cosαcosβ=[cos(α+β)+cos(α-β)]/2
sinαcosβ=[sin(α+β)+sin(α-β)]/2
推導過程
 積化和差公式
積化和差公式把兩式相加得到:sin(α+β)+sin(α-β)=2sinαcosβ
所以,sinαcosβ=[sin(α+β)+sin(α-β)]/2
同理,把兩式相減,得到:cosαsinβ=[sin(α+β)-sin(α-β)]/2
cos(α+β)=cosαcosβ-sinαsinβ,cos(α-β)=cosαcosβ+sinαsinβ
把兩式相加,得到:cos(α+β)+cos(α-β)=2cosαcosβ
所以,cosαcosβ=[cos(α+β)+cos(α-β)]/2
同理,兩式相減,得到sinαsinβ=-[cos(α+β)-cos(α-β)]/2
這樣,得到了積化和差的四個公式:
sinαcosβ=[sin(α+β)+sin(α-β)]/2
cosαcosβ=[cos(α+β)+cos(α-β)]/2
sinαsinβ=-[cos(α+β)-cos(α-β)]/2
cosαsinβ=[sin(α+β)-sin(α-β)]/2
記憶方法
積化和差公式的形式比較複雜,記憶中以下幾個方面是難點,下面指出了特點各自的簡單記憶方法。
這一點最簡單的記憶方法是通過三角函式的值域來判斷。sin和cos的值域都是[-1,1],其和差的值域應該是[-2,2],而積的值域卻是[-1,1],因此除以2是必須的。
也可以通過其證明來記憶,因為展開兩角和差公式後,未抵消的兩項相同而造成有係數2,如:
cos(α-β)-cos(α+β)
=(cosαcosβ+sinαsinβ)-(cosαcosβ-sinαsinβ)
=2sinαsinβ
故最後需要除以2。
注意事項
無論乘積項中的三角函式是否同名,化為和差形式時,都應是同名三角函式的和差。這一點主要是根據證明記憶,因為如果不是同名三角函式,兩角和差公式展開後乘積項的形式都不同,就不會出現相抵消和相同的項,也就無法化簡下去了。
使用哪種三角函式的和差仍然要根據證明記憶。注意兩角和差公式中,餘弦的展開中含有兩對同名三角函式的乘積,正弦的展開則是兩對異名三角函式的乘積。所以反過來,同名三角函式的乘積,化作餘弦的和差;異名三角函式的乘積,化作正弦的和差。
是和還是差?這是積化和差公式的使用中最容易出錯的一項。規律為:“小角”β以cosβ的形式出現時,乘積化為和;反之,則乘積化為差。
由函式的奇偶性記憶這一點是最便捷的。如果β的形式是cosβ,那么若把β替換為-β,結果應當是一樣的,也就是含α+β和α-β的兩項調換位置對結果沒有影響,從而結果的形式應當是和;另一種情況可以類似說明。
正弦-正弦積公式的負號是一個特殊情況,必須記牢。
當然,也有其他方法可以幫助這種情況的判定,如[0,π]內餘弦函式的單調性。因為這個區間內餘弦函式是單調減的,所以cos(α+β)不大於cos(α-β)。但是這時對應的α和β在[0,π]的範圍內,其正弦的乘積應大於等於0,所以要么反過來把cos(α-β)放到cos(α+β)前面,要么就在式子的最前面加上負號。
積化和差套用
積化和差公式可以將兩個三角函式值的積化為另兩個三角函式值的和乘以常數的形式,所以使用積化和差公式可以達到降次的效果。
在歷史上,對數出現之前,積化和差公式被用來將乘除運算化為加減運算,運算需要利用三角函式表。
運算過程:將兩個數通過乘、除10的方冪化為0到1之間的數,通過查表求出對應的反三角函式值,即將原式化為10^k*sinαsinβ的形式,套用積化和差後再次查表求三角函式的值,並最後利用加減算出結果。對數出現後,積化和差公式的這個作用由更加便捷的對數取代。
在現代工程中,積化和差的重要套用在於求解傅立葉級數,特別是在以2π為周期和以2L為周期的函式展開為傅立葉級數時。因為在這種情況下,被展開函式f(x)一般也是三角函式,但其ω與傅立葉係數公式中的三角函式不同,這就為最終求解係數帶來很大困難,因為求解係數的過程中,要求一個在2π周期內的積分,若被積函式是cosxcosnx,直接積分非常困難,若運用積化和差將乘積的積分化為加減運算的積分,將使問題變得容易解決,使用計算機處理時效率也會更高。