等比數列求和公式

一個數列，如果任意的後一項與前一項的比值是同一個常數（這個常數通常用q來表示），且數列中任何項都不為0，即：A(n+1)/A(n)=q (n∈N*)，這個數列叫等比數列，其中常數q 叫作公比。等比數列求和公式為：Sn=n*a1(q=1) Sn=a1(1-q^n)/(1-q) =(a1-anq)/(1-q) （q不等於1）如果一個數列從第2項起，每一項與它的前一項的比等於同一個常數，這個數列就叫做等比數列。這個常數叫做等比數列的公比，公比通常用字母q表示(q≠0)，等比數列a1≠0。註：q=1時，an為常數列。利用等比數列求和公式可以快速的計算出該數列的和。

基本信息

• 中文名稱：等比數列求和公式
• 外文名：Geometric series summation formula
• 別稱：等比數列
• 表達式：an=a1×q^(n-1)

等比數列

a（n+1）/an=q,n為自然數。

通項公式

an=a1*q^（n－1）。

推廣式

an=am·q^(n－m)

求和公式

Sn=n*a1(q=1)

Sn=a1(1-q^n)/(1-q)=(a1-anq)/(1-q)（q不等於1）

性質

等比數列的性質

①若m、n、p、q∈N，且m＋n=p＋q，則am·an=ap*aq；

②在等比數列中，依次每k項之和仍成等比數列。

“G是a、b的等比中項”“G^2=ab（G≠0）”.

在等比數列中，首項A1與公比q都不為零。

注意

上述公式中A^n表示A的n次方。

n種求法

錯位相消法

教材中介紹的方法叫做“錯位相消法”。這個方法不僅可以用於等比數列，還可以用於等比數列與等差數列乘積的求和。

不同的方法

這裡用不同的方法來證明這一公式的成立。首先要知道等比數列的求和公式，下面的方法有的是求解，有的是證明
在這裡要說明點的是，如果從極限的觀點來看，當q=1與q≠1的時候，兩個公式可以合二為一，具體可以參考《等比數列求和公式的統一》一文。一開始講的，當然就是書本上的錯位相消法了。為了方便起見，下面的證明過程只考慮q≠1的情況。

錯位相消法(求解)

利用等比數列的定義：an+1=qan,有下面的式子成立；

比例法(求解)

根據等比數列的性質，an+1/an=q，所以有下面的式子成立；

裂項求和法(求解)

這個方法主要是對數列的通項公式進行變形，使之可以進行裂項求和；

指數函式法

指數函式

這個方法是看到等比數列的通項公式是一個類似指數函式，從而可以通過構造函式的方法求得數列求和公式，構造函式f(x)=a1qx.則f(x+1)-f(x)=a1(q-1)qx.所以有下面的式子成立：

f(1)-f(0)=a1(q-1)q0.

f(2)-f(1)=a1(q-1)q1.

f(3)-f(2)=a1(q-1)q2.

……………………

f(n)-f(n-1)=a1(q-1)qn-1.

將上述各式左右相加並化簡得：

f(n)-f(0)=a1(q-1)(q0+q1+q2+……+qn-1)=(q-1)Sn

而f(n)=a1qn,f(0)=1，帶入即可得到等比數列求和公式。方

程法(求解)

此方法是構造兩個關於Sn的方程，通過求解方程的方法求解Sn，消去Sn-1，解這方程組即可得Sn。

反向思維法(證明)

這種方法主要就是運用公式an-bn=(a-b)(an-1+an-2b+an-3b2+……+bn-1)

特徵方程法

還有一個特徵方程法，特徵方程是一個非常有用的工具，特別是在求解斐波拉契數列的通項公式中，特徵方程起了非常大的作用。

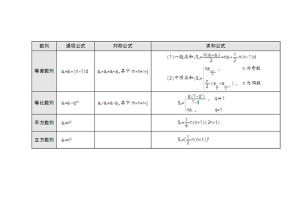等比數列求和公式