計算方法圓面積公式
怎樣求圓面積?這已是一個非常簡單的問題,用公式一算,結論就出來了。可是你可知道這個公式是怎樣得來的嗎?在過去漫長的年代裡,人們為了研究和解決這個問題,不知遇到了多少困苦,花費了多少精力和時間。在平面圖形中,以長方形的面積最容易計算了。用大小一樣的正方形磚鋪墊長方形地面,如果橫向用八塊,縱向用六塊,那一共就用了8×6=48塊磚。所以求長方形面積的公式是:長×寬。
求平行四邊形的面積,可以用割補的方法,把它變成一個與它面積相等的長方形。長方形的長和寬,就是平行四邊形的底和高。所以求平行四邊形面積的公式是:底×高。
求三角形的面積,可以對接上一個和它全等的三角形,成為一個平行四邊形。這樣,三角形的面積,就等於和它同底同高的平行四邊形面積的一半。因此,求三角形面積的公式是:底×高÷2
任何一個多邊形,因為可以分割成若干個三角形,所以它的面積,就等於這些三角形面積的和。
歷史上諸多求解方法
4000多年前修建的埃及胡夫金字塔,底座是一個正方形,占地52900m2。它的底座邊長和角度計算十分準確,誤差很小,可見當時測算大面積的技術水平已經很高。
圓是最重要的曲邊形。古埃及人把它看成是神賜予人的神聖圖形。怎樣求圓的面積,是數學對人類智慧的一次考驗。
你會想,既然正方形的面積那么容易求,我們只要想辦法做出一個正方形,使它的面積恰好等於圓面積就行了。是啊,這樣的確很好,但是怎樣才能做出這樣的正方形呢?
知道古代三大幾何難題嗎?其中的一個,就是剛才講到的化圓為方。這個起源於古希臘的幾何作圖題,在2000多年裡,不知難倒了多少能人,直到19世紀,人們才證明了這個幾何題,是根本不可能用古代人的尺規作圖法作出來的。
各種求解方法
我國古代的數學家祖沖之,從圓內接正六邊形入手,讓邊數成倍增加,用圓內接正多邊形的面積去逼近圓面積。古希臘的數學家,從圓內接正多邊形和外切正多邊形同時入手,不斷增加它們的邊數,從里外兩個方面去逼近圓面積。
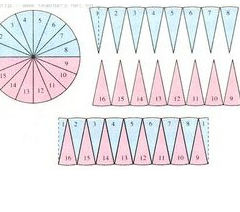
古印度的數學家,採用類似切西瓜的辦法,把圓切成許多小瓣,再把這些小瓣對接成一個長方形,用長方形的面積去代替圓面積。
眾多的古代數學家煞費苦心,巧妙構思,為求圓面積作出了十分寶貴的貢獻。為後人解決這個問題開闢了道路。
克卜勒的求解方法
16世紀的德國天文學家開普勒,是一個愛觀察、肯動腦筋的人。他把丹麥天文學家第谷遺留下來的大量天文觀測資料,認真地進行整理分析,提出了著名的“克卜勒三定律”。克卜勒第一次告訴人們,地球圍繞太陽運行的軌道是一個橢圓,太陽位於其中的一個焦點上。提出圓面積公式
克卜勒當過數學老師,他對求面積的問題非常感興趣,曾進行過深入的研究。他想,古代數學家用分割的方法去求圓面積,所得到的結果都是近似值。為了提高近似程度,他們不斷地增加分割的次數。但是,不管分割多少次,幾千幾萬次,只要是有限次,所求出來的總是圓面積的近似值。要想求出圓面積的精確值,必須分割無窮多次,把圓分成無窮多等分才行。
克卜勒也仿照切西瓜的方法,把圓分割成許多小扇形;不同的是,他一開始就把圓分成無窮多個小扇形。
圓面積等於無窮多個小扇形面積的和,所以
在最後一個式子中,各段小弧相加就是圓的周長2πR,所以有
這就是我們所熟悉的圓面積公式。
克卜勒運用無窮分割法,求出了許多圖形的面積。1615年,他將自己創造的這種求圓面積的新方法,發表在《葡萄酒桶的立體幾何》一書中。
克卜勒大膽地把圓分割成無窮多個小扇形,並果敢地斷言:無窮小的扇形面積,和它對應的無窮小的三角形面積相等。他在前人求圓面積的基礎上,向前邁出了重要的一步。
《葡萄酒桶的立體幾何》一書,很快在歐洲流傳開了。數學家們高度評價克卜勒的工作,稱讚這本書是人們創造求圓面積和體積新方法的靈感源泉。
新的理論
一種新的理論,在開始的時候很難十全十美。克卜勒創造的求圓面積的新方法,引起了一些人的懷疑。他們問道:克卜勒分割出來的無窮多個小扇形,它的面積究竟等於不等於零?如果等於零,半徑OA和半徑OB就必然重合,小扇形OAB就不存在了;如果客觀存在的面積不等於零,小扇形OAB與小三角形OAB的面積就不會相等。克卜勒把兩者看作相等就不對了。
面對別人提出的問題,克卜勒自己也解釋不清。
卡瓦利里的求解方法
他是義大利物理學家伽利略的學生,他研究了克卜勒求圓面積方法存在的問題。卡瓦利里想,克卜勒把圓分成無窮多個小扇形,這每個小扇形的面積到底等不等於圓面積,就不好確定了。但是,只要小扇形還是圖形,它是可以再分的呀。克卜勒為什麼不再繼續分下去了呢?要是真的再細分下去,那分到什麼程度為止呢?這些問題,使卡瓦利里陷入了沉思之中。
有一天,當卡瓦利里的目光落在自己的衣服上時,他忽然靈機一動:唉,布不是可以看成為面積嘛!布是由棉線織成的,要是把布拆開的話,拆到棉線就為止了。我們要是把面積像布一樣拆開,拆到哪兒為止呢?應該拆到直線為止。幾何學規定直線沒有寬度,把面積分到直線就應該不能再分了。於是,他把不能再細分的東西叫做“不可分量”。棉線是布的不可分量,直線是平面面積的不可分量。
卡瓦利里還進一步研究了體積的分割問題。他想,可以把長方體看成為一本書,組成書的每一頁紙,應該是書的不可分量。這樣,平面就應該是長方體體積的不可分量。幾何學規定平面是沒有薄厚的,這樣也是有道理的。
新的求解方法
卡瓦利里緊緊抓住自己的想法,反覆琢磨,提出了求圓面積和體積的新方法。1635年,當《葡萄酒桶的立體幾何》一書問世20周年的時候,義大利出版了卡瓦利里的《不可分量幾何學》。在這本書中,卡瓦利里把點、線、面,分別看成是直線、平面、立體的不可分量;把直線看成是點的總和,把平面看成是直線的總和,把立體看成是平面的總和。
卡瓦利里還根據不可分量的方法指出,兩本書的外形雖然不一樣,但是,只要頁數相同,薄厚相同,而且每一頁的面積也相等,那么,這兩本書的體積就應該相等。他認為這個道理,適用於所有的立體,並且用這個道理求出了很多立體的體積。這就是有名的“卡瓦利里原理。”
事實上,最先提出這個原理的,是我國數學家祖沖之。比卡瓦利里早1000多年,所以我們叫它“祖沖之原理”或者“祖沖之定理”。
在一個圓里畫一個最大的正方形,正方形占圓面積的約63.7%,在一個圓外畫一個最小的正方形,正方形面積是圓形面積的157%。
推導
圓周長公式的推導:
我們學過π等於圓周長(c):圓的直徑(D),圓的半徑(R)那圓的周長(c)除以圓的直徑(R)等於π,那利用乘法的意義,就等於π乘以圓的直徑(R)等於圓的周長(C),C=πd。而同園的直徑(R)是圓的半徑(r)的兩倍,所以就圓的周長(c)等於2乘以π乘以圓的半徑(r),C=2πr。
圓面積公式的推導:
把圓平均分成若干份,可以拼成一個近似的長方形。長方形的寬就等於圓的半徑(r),長方形的長就是圓周長(C)的一半。長方形的面積是s=ab,那圓的面積就是:圓的半徑(r)的平方乘以π,S=πr²。
圓面積公式
圓的半徑=r直徑=d
圓周率(π)設為3.14
(圓面積)S圓=πr²
(圓周長)S圓=πd
s圓=πr²
公式推導
圓周長公式的推導[3]圓周長(C):圓的直徑(d),那圓的周長(C)除以圓的直徑(d)等於π,那利用乘法的意義,就等於π乘以圓的直徑(d)等於圓的周長(C),C=πd。而同圓的直徑(d)是圓的半徑(r)的兩倍,所以就圓的周長(C)等於2乘以π乘以圓的半徑(r),C=2πr。
圓面積公式的推導
把圓平均分成若干份,可以拼成一個近似的長方形。長方形的寬就等於圓的半徑(r),長方形的長就是圓周長(C)的一半。長方形的面積是ab,那圓的面積就是:圓的半徑(r)的平方乘以π,S=πrr。
其他信息
計算方法怎樣求圓面積?這已是一個非常簡單的問題,用公式一算,結論就出來了。可是你可知道這個公式是怎樣得來的嗎?在過去漫長的年代裡,人們為了研究和解決這個問題,不知遇到了多少困苦,花費了多少精力和時間。
在平面圖形中,以長方形的面積最容易計算了。用大小一樣的正方形磚鋪墊長方形地面,如果橫向用八塊,縱向用六塊,那一共就用了8×6=48塊磚。所以求長方形面積的公式是:長×寬。
求平行四邊形的面積,可以用割補的方法,把它變成一個與它面積相等的長方形。長方形的長和寬,就是平行四邊形的底和高。所以求平行四邊形面積的公式是:底×高。
求三角形的面積,可以對接上一個和它全等的三角形,成為一個平行四邊形。這樣,三角形的面積,就等於和它同底同高的平行四邊形面積的一半。因此,求三角形面積的公式是:底×高÷2
任何一個多邊形,因為可以分割成若干個三角形,所以它的面積,就等於這些三角形面積的和。
歷史上諸多求解方法
4000多年前修建的埃及胡夫金字塔,底座是一個正方形,占地52900m2。它的底座邊長和角度計算十分準確,誤差很小,可見當時測算大面積的技術水平已經很高。
圓是最重要的曲邊形。古埃及人把它看成是神賜予人的神聖圖形。怎樣求圓的面積,是數學對人類智慧的一次考驗。
也許你會想,既然正方形的面積那么容易求,我們只要想辦法做出一個正方形,使它的面積恰好等於圓面積就行了。是啊,這樣的確很好,但是怎樣才能做出這樣的正方形呢?
你知道古代三大幾何難題嗎?其中的一個,就是剛才講到的化圓為方。這個起源於古希臘的幾何作圖題,在2000多年裡,不知難倒了多少能人,直到19世紀,人們才證明了這個幾何題,是根本不可能用古代人的尺規作圖法作出來的。
我國古代的數學家祖沖之,從圓內接正六邊形入手,讓邊數成倍增加,用圓內接正多邊形的面積去逼近圓面積。
古希臘的數學家,從圓內接正多邊形和外切正多邊形同時入手,不斷增加它們的邊數,從里外兩個方面去逼近圓面積。
古印度的數學家,採用類似切西瓜的辦法,把圓切成許多小瓣,再把這些小瓣對接成一個長方形,用長方形的面積去代替圓面積。
眾多的古代數學家煞費苦心,巧妙構思,為求圓面積作出了十分寶貴的貢獻。為後人解決這個問題開闢了道路。
面對別人提出的問題,克卜勒自己也解釋不清。
卡瓦利里的求解方法
他是義大利物理學家伽利略的學生,他研究了克卜勒求圓面積方法存在的問題。
卡瓦利里想,克卜勒把圓分成無窮多個小扇形,這每個小扇形的面積到底等不等於圓面積,就不好確定了。但是,只要小扇形還是圖形,它是可以再分的呀。克卜勒為什麼不再繼續分下去了呢?要是真的再細分下去,那分到什麼程度為止呢?這些問題,使卡瓦利里陷入了沉思之中。
有一天,當卡瓦利里的目光落在自己的衣服上時,他忽然靈機一動:唉,布不是可以看成為面積嘛!布是由棉線織成的,要是把布拆開的話,拆到棉線就為止了。我們要是把面積像布一樣拆開,拆到哪兒為止呢?應該拆到直線為止。幾何學規定直線沒有寬度,把面積分到直線就應該不能再分了。於是,他把不能再細分的東西叫做“不可分量”。棉線是布的不可分量,直線是平面面積的不可分量。
卡瓦利里還進一步研究了體積的分割問題。他想,可以把長方體看成為一本書,組成書的每一頁紙,應該是書的不可分量。這樣,平面就應該是長方體體積的不可分量。幾何學規定平面是沒有薄厚的,這樣也是有道理的。
新的求解方法
卡瓦利里緊緊抓住自己的想法,反覆琢磨,提出了求圓面積和體積的新方法。
1635年,當《葡萄酒桶的立體幾何》一書問世20周年的時候,義大利出版了卡瓦利里的《不可分量幾何學》。在這本書中,卡瓦利里把點、線、面,分別看成是直線、平面、立體的不可分量;把直線看成是點的總和,把平面看成是直線的總和,把立體看成是平面的總和。
卡瓦利里還根據不可分量的方法指出,兩本書的外形雖然不一樣,但是,只要頁數相同,薄厚相同,而且每一頁的面積也相等,那么,這兩本書的體積就應該相等。他認為這個道理,適用於所有的立體,並且用這個道理求出了很多立體的體積。這就是有名的“卡瓦利里原理。”
事實上,最先提出這個原理的,是我國數學家祖沖之。比卡瓦利里早1000多年,所以我們叫它“祖沖之原理”或者“祖沖之定理”。
在一個圓里畫一個最大的正方形,正方形占圓面積的約63.7%,在一個圓外畫一個最小的正方形,正方形面積是圓形面積的157%。