直線的一般式方程
直線的一般式方程能夠表示坐標平面內的任何直線。
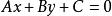 直線的一般式方程
直線的一般式方程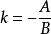 直線的一般式方程
直線的一般式方程(A,B不全為零即A^2+B^2≠0)該直線的斜率為 (當B=0時沒有斜率)
平行於x軸時,A=0,C≠0;
平行於y軸時,B=0,C≠0;
與x軸重合時,A=0,C=0;
與y軸重合時,B=0,C=0;
過原點時,C=0;
與x、y軸都相交時,A*B≠0。
關於直線的一般式方程的結論
 直線的一般式方程
直線的一般式方程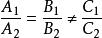 直線的一般式方程
直線的一般式方程兩直線平行時:普遍適用: ,方便記憶運用: (A2B2C2 != 0)
 直線的一般式方程
直線的一般式方程兩直線垂直時:
 直線的一般式方程
直線的一般式方程兩直線重合時: ()
 直線的一般式方程
直線的一般式方程 直線的一般式方程
直線的一般式方程兩直線相交時: ()
兩直線一般式垂直公式的證明:設直線l1:A1x+B1y+C1=0直線l2:A2x+B2y+C2=0
(必要性)∵l1⊥l2∴k1×k2=-1∵k1=-B1/A1, k2=-B2/A2
∴(-B1/A1)(B2/A2)=-1 ∴(B1B2)/(A1A2)=-1
 直線的一般式方程
直線的一般式方程∴B1B2=-A1A2∴A1A2+B1B2=0
(充分性)∵A1A2+B1B2=0∴B1B2=-A1A2∴(B1B2)(1/A1A2)=-1
∴(B1/A1)(B2/A2)=-1∴(-B1/A1)(-B2/A2)=-1∵k1=-B1/A1, k2=-B2/A2
∴k1×k2=-1∴l1⊥l2
已知直線上兩點求直線的一般式方程
一般式方程在計算機領域的重要性
常用的直線方程有一般式點斜式截距式斜截式兩點式等等。除了一般式方程,它們要么不能支持所有情況下的直線(比如跟坐標軸垂直或者平行),要么不能支持所有情況下的點(比如x坐標相等,或者y坐標相等)。所以一般式方程在用計算機處理二維圖形數據時特別有用。
已知直線上兩點求直線的一般式方程
已知直線上的兩點P1(X1,Y1) P2(X2,Y2), P1 P2兩點不重合。
對於AX+BY+C=0:
當x1=x2時,直線方程為x-x1=0
當y1=y2時,直線方程為y-y1=0
當x1≠x2,y1≠y2時,直線的斜率k=(y2-y1)/(x2-x1)
故直線方程為y-y1=(y2-y1)/(x2-x1)×(x-x1)
即x2y-x1y-x2y1+x1y1=(y2-y1)x-x1(y2-y1)
即(y2-y1)x-(x2-x1)y-x1(y2-y1)+(x2-x1)y1=0
即(y2-y1)x+(x1-x2)y+x2y1-x1y2=0 ①
可以發現,當x1=x2或y1=y2時,①式仍然成立。所以直線AX+BY+C=0的一般式方程就是:
A = Y2 - Y1
B = X1 - X2
C = X2*Y1 - X1*Y2

