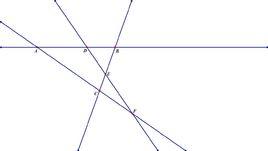
常規解法
若已知直線過兩點(x1,y1)和(x2,y2),求該直線解析式。
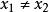 直線解析式
直線解析式若 ,設該直線解析式為y=kx+b,將點(x1,y1)和(x2,y2)代入該解析式中,得:
 直線解析式
直線解析式,
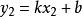 直線解析式
直線解析式,
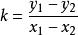 直線解析式
直線解析式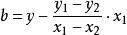 直線解析式
直線解析式解方程組, , ;
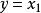 直線解析式
直線解析式否則,直線解析式為 。
表示形式
一般式
適用於所有直線 Ax+By+C=0 (其中A、B不同時為0)。
點斜式
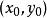 直線解析式
直線解析式 直線解析式
直線解析式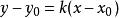 直線解析式
直線解析式若已知直線上一點 ,並且所求直線的斜率 存在,則直線可表示為: 。
 直線解析式
直線解析式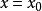 直線解析式
直線解析式當 不存在時,直線可表示為 。
斜截式
 直線解析式
直線解析式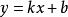 直線解析式
直線解析式 直線解析式
直線解析式若在y軸上截距為b(即過(0,b)),斜率為 的直線,由點斜式可得斜截式: 。與點斜式一樣,也需要考慮 不存在的情況
截矩式
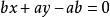 直線解析式
直線解析式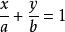 直線解析式
直線解析式若已知直線與x軸交於(a,0),與y軸交於(0,b),則直線可表示為: 。特別地,當ab均不為0時,斜截式可寫為 。
需注意的是,它不適用於和任意坐標軸垂直的直線。
兩點式
 直線解析式
直線解析式若已知該直線過點(x1,y1)和(x2,y2),且斜率k存在,則兩點式解析式是: 。
法線式
 直線解析式
直線解析式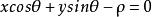 直線解析式
直線解析式若已知 為原點到直線的距離,θ為法線與X軸正方向的夾角,則 。
點方向式
 直線解析式
直線解析式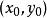 直線解析式
直線解析式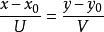 直線解析式
直線解析式若已知直線的方向向量為 ,並過點 ,則 。
距離計算
點到直線距離
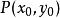 直線解析式
直線解析式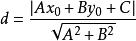 直線解析式
直線解析式點 到直線Ι:Ax+By+C=0的距離: 。
兩平行線之間距離
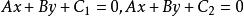 直線解析式
直線解析式若兩平行直線的方程分別為: ,則這兩條平行直線間的距離為:
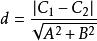 直線解析式
直線解析式。