直線系

直線系(system of straight lines)亦稱直線束，是具有某一共同性質的直線的集合。如在平面仿射坐標系中，與已知直線Ax+By+C=0平行的所有直線組成一個直線系，它的方程為Ax+By+λ=0，式中λ是參數。又如，通過一個定點(x0，y0)的所有直線也是一個直線系，稱為以(x0，y0)為束心的直線束，它的方程為λ1(x-x0)+λ2(y-y0)=0，式中λ1，λ2是不同時為零的參數。如果只用一個參數來表示，直線束的方程為y-y0=k(x-x0)，式中k為參數，但此直線束不包含直線x=x0。一般地，對於給定的兩直l1： A1x+B1y+C1=0，l2： A2x+B2y+C2=0，含有參數λ1，λ2(不同時為零)的方程λ1(A1x+B1y+C1)+λ2(A2x+B2y+C2)=0表示由l1和l2決定的直線束，並且：1.當l1與l2相交時，是以l1與l2的交點為中心的直線束，稱為中心直線束；2.當l1與l2平行(但不重合)時，該直線束稱為平行直線束，且當參數λ1，λ2取值為同號或異號時，所對應的直線位於直線l1與l2之間或之外 。

定義

直線系是指具有某種共同特徵的直線的集合，表示這個直線系的方程叫做 直線系方程，其特點是在直線方程中含有一個參數。

確定平面上一條直線，需要兩個獨立且相容的幾何條件，如果只給定一個條件，直線的位置不能完全確定。另一方面，如果只給定一個幾何條件時，二元一次方程的兩個獨立的係數中，只有一個被確定，那個未被確定的係數是參數。

利用直線系方程求直線，可以簡化計算過程，欲求適合某兩個幾何條件的直線的方程，可先用其中一個條件寫出直線系方程，再用另一個條件來確定參數值 。

常見的直線系方程

常見的直線系方程有以下幾種：

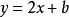直線系

（1）有共同斜率的直線系方程。如斜率為2的直線系方程為 (b為參數)。

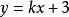直線系

直線系

（2）在 軸上共截距的直線系方程。如截距為3的直線系方程為 (k為參數)。

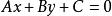直線系

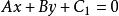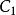直線系

直線系

（3）與直線 平行的直線系方程為 ( 為參數)。

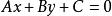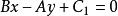直線系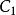

直線系

直線系

（4）與直線 垂直的直線系方程為 ( 為參數)。

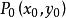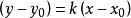直線系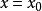

直線系

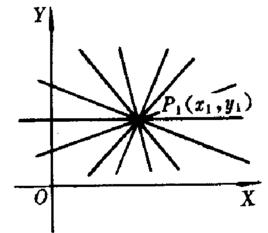
直線系

（5）過已知點 的直線系方程為 (k為參數)，不含直線 。

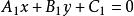直線系

直線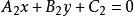系

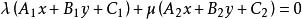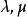直線系

直線系

（6）過兩直線 及 交點的直線系方程為 ( 是不全為零的實數)。

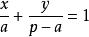直線系

直線系

（7）在兩軸上截距之和為定值p的直線系： （ 為參數）。

套用

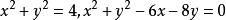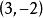直線系

直線系

例1 給出兩圓 和一點 ，求通過兩圓交點和這點的圓。

解： 不用解聯立方程求出兩圓交點，再求通過三點的圓，這樣做工作量相當大。

凡是通過兩已知圓交點的圓的方程必呈下形式

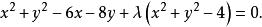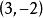直線系

直線系

要求此圓通過點 得

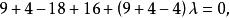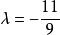直線系

直線系

所以 代入上式得所求圓

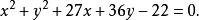直線系

例2 求三角形外接圓的方程，已知三角形三邊的方程為

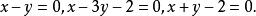直線系

解： 按通常的解法，先解三個二元一次方程組，以得出三角形三個頂點的坐標；再按三個條件列出一個三元一次方程組並解出所求圓的係數來，才得出所求圓的方程。

有了直線系和曲線系的啟示，這裡設計一個新解法：

對於一切實數a和b，二次曲線

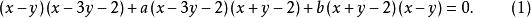直線系

直線系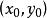

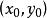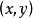直線系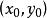

直線系

直線系

必通過三邊兩兩交點。這是因為：設 是一個頂點，以 代替 ，它使這裡出現的三個不同的括弧中的兩個為零，因而上式左端三項都為零，可見曲線(1)通過，即通過任一頂點。

進一步要使二次曲線(1)代表圓，二次曲線是圓的充要條件是兩條：

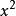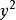直線系

直線系

(1)的係數= 的係數；

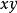直線系

(2)的係數=0 。

於是得

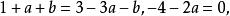直線系

所以

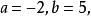直線系

代入式(1)，乘出得所求外接圓的方程為

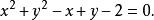直線系