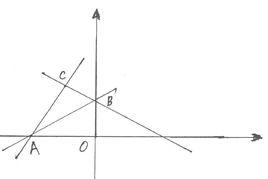
直線的一般式
定義
在平面直角坐標系中,任何一個關於x,y的二元一次方程Ax+By+C=0(A,B不全為0)都表示一條直線。
我們把簡稱方程:Ax+By+C=0(其中A、B不同時為0)叫做直線方程的一般式。
意義
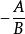 一般式
一般式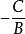 一般式
一般式直線方程的一般式中,在B不等於0的情況下,代表了該直線的斜率,代表直線在y軸上的截距。
 一般式
一般式而B等於0時,直線的斜率就不存在(或為無窮大)。此時,直線與x軸垂直,直線的方程也可以化為
證明
對於任意一個二元一次方程Ax+By+C=0(A,B不同時為零)判斷它是否表示一條直線,就看能否把它化成直線方程的某一種形式。
 一般式
一般式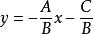 一般式
一般式當時,該方程可變為:。
而這是直線方程的斜截式(y=kx+b)。
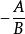 一般式
一般式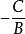 一般式
一般式所以直線的一般式能代表一條直線,它的斜率為,而它在y軸上的截距為,在x軸上的截距為-C/A。
特殊情況
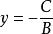 一般式
一般式(1)平行於x軸時,A=0 B≠0 C≠0
 一般式
一般式⑵平行於y軸時,A≠0 B=0 C≠0
⑶與x軸重合時,A=0 B≠0 C=0 y=0
⑷與y軸重合時,A≠0 B=0 C=0 x=0
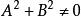 一般式
一般式⑸過原點時,C=0,
相關結論
兩直線平行時:普遍適用:A1B2=A2B1,方便記憶運用:A1/A2=B1/B2≠C1/C2 ( A2*B2*C2≠0)[1]
兩直線垂直時:A1A2+B1B2=0
兩直線重合時:A1/A2=B1/B2=C1/C2 ( A2*B2*C2≠0)
兩直線相交時:A1/A2≠B1/B2 ( A2*B2≠0)
相關公式定理
點到直線距離公式
 一般式
一般式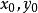 一般式
一般式分點
()到直線l:Ax+By+C=0(也就是該直線的一般式)的距離公式為: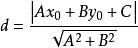 一般式
一般式平行線之間的距離公式為:
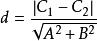 一般式
一般式其他形式
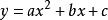 一般式
一般式二次函式一般式()(a不等於0)已知三點求二次函式解析式(]]y=ax^2b]i]]]+bx+cb]i])可設二次函式解析式為:y=ax2+bx+c知道3點了,分別代入這個解析式,就可以得出3個方程,3個方程,3個未知數,就可以求出a,b,c了還有就是,如果3個交點中有2個交點是二次函式與x軸的交點那么,可設這個二次函式解析式為:y=a(x-x1)(x-x2)(x1,x2是二次函式與x軸的2個交點坐標),根據另一個點就可以求出二次函式解析式如果知道頂點坐標為(h,k),則可設:y=a(x-h)2+k,根據另一點可求出二次函式解析式