定義
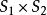環面定義一：與 同胚的曲面稱為環面，它是虧格為1的可定向閉曲面。通常，環面可以看作由一個長方體按照逆時針方向分別疊合左右兩邊和上下兩邊而得到的。
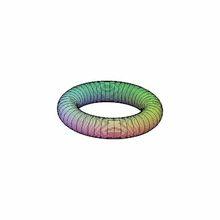圖1定義二：若一個線性代數群G同構於某個D(n,k)，則稱G是一個環面。連通的可對角化代數群一定是一個環面。
幾何意義
在幾何上，一個 環面是一個麵包圈形狀的旋轉曲面，由一個圓繞一個和該圓共面的一個軸迴轉所生成。球可以視為環面的特殊情況，也就是旋轉軸是該圓的直徑時。若轉軸和圓不相交，圓面中間有一個洞，就像一個圈形麵包圈，一個呼啦圈，或者一個充了氣的輪胎面。另一個情況，也就是軸是圓的一根弦的時候，就產生一個擠扁了的球面，就像一個圓的座墊那樣。
環面可以參數式地定義為：
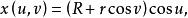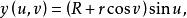環面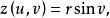
環面
環面其中 u, v ∈ [0, 2π], R是管子的中心到畫面的中心的距離， r是圓管的半徑。
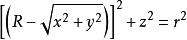環面直角坐標系中的關於z-軸方位角對稱的環面方程是：。
該圓環面的表面積和內部體積如下：
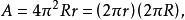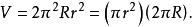環面
環面根據更一般的定義，環面的生成元不必是圓，而可以是橢圓或任何圓錐曲線。
拓撲
拓撲學上，一個 環面是一個定義為兩個圓的積的閉合曲面。
n維環面
代數群的一個重要子群。指與n階可逆對角矩陣全體所成的群D(n，K)同構的代數群。環面的有理表示都是完全可約的，不可約表示都是一維的。所以環面的表示理論被特徵標群完全刻畫。一個代數群中的極大環面子群(簡稱極大環面)在這個代數群的結構與表示理論中起著至關重要的作用。不同的極大環面在代數群中是互相共軛的。
生產套用
圖2環面透鏡是相當於在環面體邊緣切削的一塊帽狀透鏡。透鏡表面的形狀像甜甜圈邊緣削掉的一塊。最高的和最低的兩個曲率都是圓弧曲率。因此，與一個非常流行的看法不同，環面透鏡並不是一個橢球面。主要用於隱形眼鏡,角膜塑形鏡和人工晶體，從而矯正高度角膜散光。
