理想飽和通行能力

Ri=niQsi（Gei/C）=niQsiλi （02.8-5）

式中：Ri：車流i的飽和通行能力，（pcu/h）；

ni：車流i的進口車道數量；

Qsi：車流i的腳踏車道飽和流率，（pcu/h）；

C：周期，（s）；

Gei：車流i的有效綠燈時間，（s）；

λi：車流i的綠信比。

理想飽和通行能力：信號交叉口某進口道的理想飽和通行能力滿足計算式：
Ri=niQsi（Gei/C）=niQsiλi（02.8-5）
式中：Ri：車流i的飽和通行能力，（PCU/h）；
ni：車流i的進口車道數量；
Qsi：車流i的腳踏車道飽和流率，（pcu/h）；
C：周期，（s）；
Gei：車流i的有效綠燈時間，（s）；
λi：車流i的綠信比。
必要說明
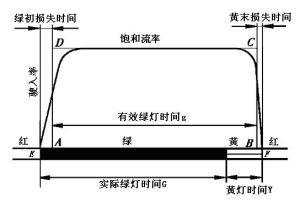
車流通過停車線的基本運動特性如圖1所示，實際上表示的是停車線截面上駛入流率-時間的變化情況。其基本模式是由克萊頓（Clayton）於1940-1941年提出來的。後來，沃喬普（Wardrop），韋伯斯特和柯布（Cobbe）等學者沿用並發展了克萊頓的模式，使之成為今天我們看到的這樣一個圖式。
為了糾正綠燈間隔時間由“黃燈時間+全紅燈時間”組成的傳統錯誤概念，圖中用文字“慢車最大清空時間與快車最小進入時間的差”代替了原圖的“全紅燈時間”。
圖1所示的車流越過停車線的模式表明：當交通信號燈轉變為綠燈顯示時，原先等候在停車線後面的車流便開始向前運動，車輛魚貫地越過停車線，其流率由0很快增至一個穩定的數值，即飽和流率。此後，越過停車線的後續車流流率將繼續保持與飽和流率相等，直到停車線後面原先積存的車輛全部放行完畢，或者雖未放完，但放行時間已經截止。
從圖1可見，在綠燈信號開始的最初幾秒，流率變化很快，這是由於車流正處於起步和加速階段，在此期間，通過停車線的車流流率要比飽和流率低。同理，在綠燈結束後的黃燈期間，因嚴禁闖紅燈，有部分車輛已經開始減速，採取了制動措施，故通過停車線的車流流率便由飽和流率逐漸地降下來。
有一點值得注意，只有當綠燈期間停車線後始終保持有連續車隊時，車流越過停車線時的流率才能穩定在飽和流量水平上。圖1所表示的正是一個完全飽和的實例，即在通行結束前，始終都有車輛連續不斷地通過停車線。
圖1中矩形ABCD所包圍的面積與實曲線包圍的面積相等，恰好等於一次綠燈放行實際通過交叉口的車輛總數。矩形ABCD的高度為飽和流率，長度為有效綠燈時間，即一周期內能夠用於以飽和流率通行的時間，等於實際綠燈時間與黃燈時間的和，再去掉起動損失時間。
從圖1可以看出，綠燈信號的實際顯示時間段與有效綠燈時間區段是錯開的。在綠燈開始初期，車流難以飽和流率進入，因此損失的通行時間，稱為綠初損失時間；臨黃燈結束末期，越過停止線的車流已非飽和流率，因此損失的通行時間，稱為黃末損失時間；綠初、黃末非飽和損失時間合併稱為起動損失時間。