確定
車流通過交叉口時的基本運動特性如圖1所示，實際上表示的是停車線截面上駛入流率-時間的變化情況。其基本模式是由克萊頓（Clayton）於1940-1941年提出來的。後來，沃喬普（Wardrop），韋伯斯特和柯布（Cobbe）等學者沿用並發展了克萊頓的模式，使之成為這樣一個圖式。
公式：
g=effective green= G+Y-L
其中
g:有效綠燈時間，單位(s)
G:實際綠燈時間，單位(s)
Y:實際黃燈清空時間，單位(s)
L:損失時間，單位(s)
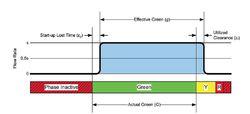圖1一般有效綠燈時間用小寫g表示，實際綠燈時間用大寫G表示，以示區分。
為了糾正綠燈間隔時間由“黃燈時間+全紅燈時間”組成的傳統錯誤概念，圖中用文字“慢車最大清空時間與快車最小進入時間的差”代替了原圖的“全紅燈時間”。
圖1所示的車流越過停車線的模式表明：當交通信號燈轉變為綠燈顯示時，原先等候在停車線後面的車流便開始向前運動，車輛魚貫地越過停車線，其流率由0很快增至一個穩定的數值，即飽和流率。此後，越過停車線的後續車流流率將繼續保持與飽和流率相等，直到停車線後面原先積存的車輛全部放行完畢，或者雖未放完，但放行時間已經截止。
從圖1可見，在綠燈信號開始的最初幾秒，流率變化很快，這是由於車流正處於起步和加速階段，在此期間，通過停車線的車流流率要比飽和流率低。同理，在綠燈結束後的黃燈期間，因嚴禁闖紅燈，有部分車輛已經開始減速，採取了制動措施，故通過停車線的車流流率便由飽和流率逐漸地降下來。
有一點值得注意，只有當綠燈期間停車線後始終保持有連續車隊時，車流越過停車線時的流率才能穩定在飽和流量水平上。圖1所表示的正是一個完全飽和的實例，即在通行結束前，始終都有車輛連續不斷地通過停車線。
圖1中矩形ABCD所包圍的面積與實曲線包圍的面積相等，恰好等於一次綠燈放行實際通過交叉口的車輛總數。矩形ABCD的高度為飽和流率，長度為有效綠燈時間，即一周期內能夠用於以飽和流率通行的時間，等於實際綠燈時間與黃燈時間的和，再去掉起動損失時間。
從圖1可以看出，綠燈信號的實際顯示時間段與有效綠燈時間區段是錯開的。在綠燈開始初期，車流難以飽和流率進入，因此損失的通行時間，稱為綠初損失時間；臨黃燈結束末期，越過停止線的車流已非飽和流率，因此損失的通行時間，稱為黃末損失時間；綠初、黃末非飽和損失時間合併稱為起動損失時間。
最大綠燈時間
在早期文獻提出的單點交通控制問題中，作為線性規劃問題，綠燈時間之和被選為最佳化目標Ⅲ]，最佳信號方案最大化了這一目標。在R. Camus et al於ⅡIAESTED論壇上發表的論文中會找到另一種類似的問題闡述，該論文關注於複雜路口的交通控制，並以其目標函式為所有信號組或所有包括到達交通流信號組綠燈時間之和作為數學規劃問題的描述。
這些目標函式表達如下：
分配給信號組D’的有效綠燈時間：
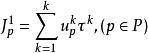有效綠燈時間分配給信號組系列P子集P的有效綠燈時間總和：
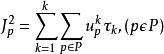有效綠燈時間綠燈時間的總和，即：分配給所有信號組的有效綠等時間總和：
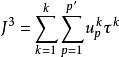有效綠燈時間所列出的帶有相應約束的最佳化目標定義了綜合最佳化問題，即：在控制向量轉換圖上尋找最佳閉合路徑以及最佳周期時間分配，對於一個給定的信號方案結構，信號方案最佳化問題簡化為確定周期時間分配。
