英文名稱
Newton'sSecondLawofMotion-ForceandAcceleration定律內容
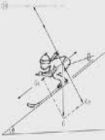 圖2
圖2公式
F合=ma (單位:N(牛)或者千克米每二次方秒) 牛頓發表的原始公式:F=d(mv)/dt(見 自然哲學之數學原理) 動量為p的物體,在合外力為F的作用下,其動量隨時間的變化率等於作用於物體的合外力。 用通俗一點的話來說,就是以t為自變數,p為因變數的函式的導數,就是該點所受的合外力。 即: F=dp/dt=d(mv)/dt (d即德爾塔,△) 而當物體低速運動,速度遠低於光速時,物體的質量為不依賴於速度的常量,所以有 F=m(dv/dt)=ma 這也叫動量定理。在相對論中F=ma是不成立的,因為質量隨速度改變,而F=d(mv)/dt依然使用。 由實驗可得在加速度一定的情況下F∝m,在質量一定的情況下F∝a (只有當F以N,m以kg,a以m/s^2為單位時,F合=ma 成立)
幾點說明
(1)牛頓第二定律是力的瞬時作用規律。力和加速度同時產生,同時變化,同時消失。 (2)F=ma是一個矢量方程,套用時應規定正方向,凡與正方向相同的力或加速度均取正值,反之取負值,一般常取加速度的方向為正方向。 (3)根據力的獨立作用原理,用牛頓第二定律處理物體在一個平面內運動的問題時,可將物體所受各力正交分解[1],在兩個互相垂直的方向上分別套用牛頓第二定律的分量形式:Fx=max,Fy=may列方程。 4.牛頓第二定律的六個性質: (1)因果性:力是產生加速度的原因。若不存在力,則沒有加速度。 (2)矢量性:力和加速度都是矢量,物體加速度方向由物體所受合外力的方向決定。牛頓第二定律數學表達式∑F = ma中,等號不僅表示左右兩邊數值相等,也表示方向一致,即物體加速度方向與所受合外力方向相同。 根據他的矢量性可以用正交分解法講力合成或分解。 (3)瞬時性:當物體(質量一定)所受外力發生突然變化時,作為由力決定的加速度的大小和方向也要同時發生突變;當合外力為零時,加速度同時為零,加速度與合外力保持一一對應關係。牛頓第二定律是一個瞬時對應的規律,表明了力的瞬間效應。 (4)相對性:自然界中存在著一種坐標系,在這種坐標系中,當物體不受力時將保持勻速直線運動或靜止狀態,這樣的坐標系叫慣性參照系。地面和相對於地面靜止或作勻速直線運動的物體可以看作是慣性參照系,牛頓定律只在慣性參照系中才成立。 (5)獨立性:物體所受各力產生的加速度,互不干擾,而物體的實際加速度則是每一個力產生加速度的矢量和,分力和分加速度在各個方向上的分量關係,也遵循牛頓第二定律。 (6)同一性:a與F與同一物體某一狀態相對應。
牛頓第二定律的適用範圍
1.當考察物體的運動線度可以和該物體的德布羅意波長相比擬時,由於測不準原理,物體的動量和位置已經是不能同時準確獲知的量了,因而牛頓動力學方程缺少準確的初始條件無法求解。也就是說經典的描述方法由於測不準原理已經失效或者需要修改。量子力學用希爾伯特空間中的態矢概念代替位置和動量(或速度)的概念來描述物體的狀態,用薛丁格方程代替牛頓動力學方程(即含有力場具體形式的牛頓第二定律)。 用態矢代替位置和動量的原因是由於測不準原理我們無法同時知道位置和動量的準確信息,但是我們可以知道位置和動量的機率分布,測不準原理對測量精度的限制就在於兩者的機率分布上有一個確定的關係。 2.由於牛頓動力學方程不是洛倫茲協變的,因而不能和狹義相對論相容,因而當物體做高速移動時需要修改力,速度,等力學變數的定義,使動力學方程能夠滿足洛倫茲協變的要求,在物理預言上也會隨速度接近光速而與經典力學有不同。 但我們仍可以引入“慣性”使牛頓第二定律的表示形式在非慣性系中使用。 例如:如果有一相對地面以加速度為a做直線運動的車廂,車廂地板上放有質量為m的小球,設小球所受的合外力為F,相對車廂的加速度為a',以車廂為參考系,顯然牛頓運動定律不成立.即 F=ma'不成立 若以地面為參考系,可得 F=ma對地 式中,a對地是小球相對地面的加速度.由運動的相對性可知 a對地=a+a' 將此式帶入上式,有 F=m(a+a')=ma+ma' 則有 F+(-ma)=ma' 故此時,引入Fo=-ma,稱為慣性力,則F+Fo=ma' 此即為在非慣性系中使用的牛頓第二定律的表達形式. 由此,在非慣性系中套用牛頓第二定律時,除了真正的和外力外,還必須引入慣性力Fo=-ma,它的方向與非慣性系相對慣性系(地面)的加速度a的方向相反,大小等於被研究物體的質量乘以a。 注意: 當物體的質量m一定時,物體所受合外力F與物體的加速度a是成正比的是錯誤的,因為是合力決定加速度。但當說是物體的質量m一定時,物體的加速度a與物體所受合外力F成正比時則是正確的。 解題技巧: 套用牛頓第二定律解題時,首先分析受力情況,運動圖景,列出各個方向(一般為正交分解)的受力的方程與運動方程。 同時,尋找題目中的幾何約束條件(如沿繩速度相等等)列出約束方程。聯立各方程得到物體的運動學方程,然後依據題目要求積分求出位移、速度等。
牛頓第二定律的套用
牛頓第二定律是經典力學的基礎和核心,是分析、研究和解決力學問題的三大法寶之一,同時也是高考考查的重點和熱點。因此,深刻理解和靈活套用牛頓第二定律是力學中非常重要的內容,下面闡述套用牛頓第二定律時的幾類典型問題,供大家參考。
連線體問題
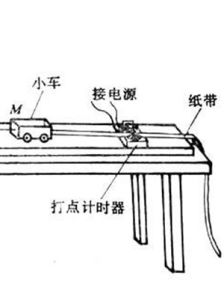
兩個或兩個以上物體相互連線並參與運動的系統稱為有相互作用力的系統,即為連線體問題,處理非平衡狀態下的有相互作用力的系統問題常常用整體法和隔離法。 當需要求內力時,常把某個物體從系統中“隔離”出來進行研究,當系統中各物體加速度相同時,可以把系統中的所有物體看成一個整體進行研究。 例1:如圖1所示的三個物體質量分別為m1、m2和m3。帶有滑輪的物體放光滑水平面上,滑輪和所有接觸面的摩擦以及繩子的質量均不計。為使三個物體無相對滑動,試求水平推力F的大小。
解答:本題是一道典型的連線體問題。 由題意可知,三個物體具有向右的相同的加速度,設為a,把它們三者看成一個整體,則這個整體在水平方向只受外力F的作用。 由牛頓第二定律,即: F=(m1+m2+m3)a ……① 隔離m2,受力如圖2所示 在豎直方向上,應有: T=m2g ……②
隔離m1,受力如圖3所示 在水平方向上,應有: T′=m1a ……③ 由牛頓第三定律T′=T ……④
聯立以上四式解得: 點評:分析處理有相互作用力的系統問題時,首先遇到的關鍵問題就是研究對象的選取。其方法一般採用隔離和整體的策略。隔離法與整體法的策略,不是相互對立的,在一般問題的求解中隨著研究對象的轉化,往往兩種策略交叉運用,相輔相成,所以我們必須具體問題具體分析,做到靈活運用。
瞬時性問題
當一個物體(或系統)的受力情況出現變化時,由牛頓第二定律可知,其加速度也將出現變化,這樣就將使物體的運動狀態發生改變,從而導致該物體(或系統)對和它有聯繫的物體(或系統)的受力發生變化。 例2:如圖4所示,木塊A與B用一輕彈簧相連,豎 直放在木塊C上。三者靜置於地面,它們的質量之比是1∶2∶3。設所有接觸面都光滑,當沿水平方向迅速抽出木塊C的瞬時,A和B的加速度aA、aB分別是多少?
解答:本題所涉及到的是彈力的瞬時變化問題。 原來木塊A和B都處受力平衡狀態,當突然抽出木塊C的瞬間,C給B的支持力將不復存在,而A、B間的彈簧還沒有來得及發生形變,仍保持原來彈力的大小和方向。 分析此題應從原有的平衡狀態入手 設木塊A的質量為m,B的質量則為2m。 抽出木塊C前木塊,A、B的受力分別如圖5、6所示。
抽出木塊C後,A的受力情況在瞬間不會發生變化,仍然保持原有的平衡狀態,則aA=0。 抽出木塊C後,對B木塊來說,N消失了。則
(方向豎直向下)
(方向豎直向下) 點評:解答瞬時性問題要把握兩個方面:一是區別“剛性繩”和“彈性繩”,當受力發生變化時前者看成形變為零,受力可以突變;後者的形變恢復需要時間,彈力的大小不能突變。二是正確分析物體在瞬間的受力情況,套用牛頓第二定律求解。
臨界問題
某一物理現象轉化為另一物理現象的轉折狀態叫臨界狀態,臨界狀態可理解為“恰好出現”或“恰好不出現”的交界狀態。處理臨界問題的關鍵是要詳細分析物理過程,根據條件變化或狀態變化,找到臨界點或臨界條件,而尋找臨界點或臨界條件常常用到極限分析的思維方法。 例3:如圖7所示,傾角為α的光滑斜面體上有一個小球m被平行於斜面的細繩繫於斜面上,斜面體放在水平面上
(1)要使小球對斜面無壓力,求斜面體運動的加速度範圍,並說明其方向。 (2)要使小球對細繩無拉力,求斜面體運動的加速度範圍,並說明其方向。 解答:為了確定小球對斜面無壓力或對細繩無拉力時斜面體的加速度,應先考慮小球對斜面體或對細繩的彈力剛好為零時的受力情況,再求出相應的加速度。 (1)分析臨界狀態,受力如圖8所示
依題則有: ∑F=ma0=mgcotα 即可得a0=gcotα 則斜面體向右運動的加速度a≥a0=gcotα(方向水平向右) (2)分析臨界狀態,受力如圖9所示。
依題意則有
(方向水平向左)即可得:
則斜面體向左運動的加速度
點評:臨界問題和極值問題是中學物理習題中的常見題型,它包含著從某一物理現象轉變為另一種物理現象,或從某一物理過程轉入另一物理過程的轉折狀態。在這個轉折點上,物理系統的某些物理量正好有臨界值。常用“最大”“最小”“剛好”“恰好”等詞語指明或暗示題中要求的臨界值或範圍。我們通常用極限分析法,首先找出發生連續性變化的物理量,將其變化推向一個或兩個極限,從而暴露其間存在的狀態與條件的關係,然後套用物理規律列式求解。
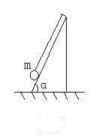 圖3
圖3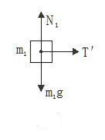 圖4
圖4 圖5
圖5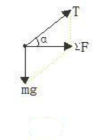 圖6
圖6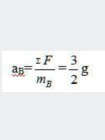 圖7
圖7