定義
如果一個系統不受外力或所受外力的矢量和為零,那么這個系統的總動量保持不變,這個結論叫做動量守恆定律。
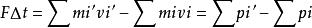 動量定理
動量定理F指合外力,如果為變力,可以使用平均值;
=既表示數值一致,又表示方向一致;
矢量求和,可以使用正交分解法;
只適用於慣性參考系,若對於非慣性參考系,必須加上慣性力的衝量。且vv必須相對於同一慣性系。
適用條件
(1)系統不受外力或系統所受的外力的合力為零。
(2)系統所受外力的合力雖不為零,但比系統內力小得多。
(3)系統所受外力的合力雖不為零,但在某個方向上的分量為零,則在該方向上系統的總動量保持不變 ——分動量守恆。
注意:(1) 區分內力和外力 碰撞時兩個物體之間一定有相互作用力,由於這兩個物體是屬於同一個系 統的,它們之間的力叫做內力;系統以外的物體施加的,叫做外力。
(2) 在總動量一定的情況下,每個物體的動量可以發生很大變化 例如:靜止的兩輛小車用細線相 連,中間有一個壓縮的彈簧。燒斷細線後,由於彈力的作用,兩輛小車分別向左右運動,它們都 獲得了動量,但動量的矢量和為零。
常見表達式
(1)p=p′ ,即系統相互作用開始時的總動量等於相互作用結束時(或某一中間狀態時)的總動量;
(2)Δp=0 ,即系統的總動量的變化為零.若所研究的系統由兩個物體組成,則可表述為: m₁v₁+m₂v₂=m₁v₁′+m₂v₂′ (等式兩邊均為矢量和);
(3)Δp₁=-Δp₂ . 即若系統由兩個物體組成,則兩個物體的動量變化大小相等,方向相反,此處要注意動 量變化的矢量性.在兩物體相互作用的過程中,也可能兩物體的動量都增大,也可能都減小,但其矢量和不變。
推導過程
推導
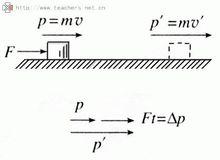 動量定理
動量定理 動量定理
動量定理將F = ma (動力學方程牛頓第二運動定律)——
代入v = v₀ + at (運動學方程)
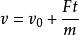 動量定理
動量定理得
化簡得mv- mv₀ = Ft
把mv做為描述物體運動狀態的量,叫動量。
含義
(1)內容:物體所受合力的衝量等於物體的動量變化。
表達式:Ft=mv′-mv=p′-p ,或Ft=△p 由此看出衝量是力在時間上的積累效應。
動量定理公式中的F是研究對象所受的包括重力在內的所有外力的合力。它可以是恆力,也可以是變力。當合外力為變力時,F是合外力對作用時間的平均值。p為物體初動量,p′為物體末動量,t為合外力的作用時間。
(2)FΔt=mΔv 是矢量式。在套用動量定理時,應該遵循矢量運算的平行四邊表法則,也可以採用正交分解法,把矢量運算轉化為標量運算。假設用Fx(或Fy)表示合外力在x(或y)軸上的分量。(或)和v (或v )表示物體的初速度和末速度在x(或y)軸上的分量,則
I=mv-mv
I=mv-mv
上述兩式表明,合外力的衝量在某一坐標軸上的分量等於物體動量的增量在同一坐標軸上的分量。在寫動量定理的分量方程式時,對於已知量,凡是與坐標軸正方向同向者取正值,凡是與坐標軸正方向反向者取負值;對於未知量,一般先假設為正方向,若計算結果為正值。說明 實際方向與坐標軸正方向一致,若計算結果為負值,說明實際方向與坐標軸正方向相反。
推廣形式
可以推廣為質點系的動量定理,即系統內動量的增量和等於合外力的衝量。
含義區別
動量定理
 動量定理
動量定理反映了力對時間的累積效應(衝量),其增量是力在時間上的積累。
動能定理
 動量定理
動量定理反映了力對空間的累積效應(功),其增量是力在空間上的積累。
動量守恆定律
m₁v₁+m₂v₂=m₁v₁'+m₂v₂'
套用
1.推廣出彈性碰撞速度表達式
對於彈性一維碰撞,我們有:
 動量定理
動量定理動能守恆 動量守恆m₁v₁+m₂v₂=m₁v₁'+m₂v₂'
可以解得:
 動量定理
動量定理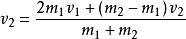 動量定理
動量定理,
2.普遍適用於物理學各個與運動相關的領域,是物體運動的基本規律。
微分形式的動量定理
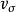 動量定理
動量定理微分形式的動量定理 若質點系的總質量為M,質心速度為 ,
 動量定理
動量定理則它的總動量為。
 動量定理
動量定理上式二邊對時間求導數,並利用質心運動定理得:,(1),
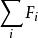 動量定理
動量定理式中為作用在質點繫上所有外力的矢量和。式(1)就是用微分形式表示的動量定理,它表明:質點系的總動量對時間的變化率等於質點系所受外力的矢量和。可以看出,質點系總動量的變化僅與外力有關,並不受質點系中各質點相互作用的內力的影響。
積分形式的動量定理
 動量定理
動量定理積分形式的動量定理積分式(1),並用p,和p,分別表示質點系在時間t和t的總動量,則有:,(2),
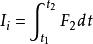 動量定理
動量定理式中為時間間隔t-t內作用於第i個質點上的外力的衝量。上式是用積分形式表示的動量定理,它表明:在某力學過程的時間間隔內,質點系總動量的改變,等於在同一時間間隔內作用於質點系所有外力的衝量的矢量和。
由於動量定理和質心運動定理是可以相互推導的,所以這兩定理在本質上是一致的。在研究剛體或剛體系統的運動時,由於質心坐標容易確定,用質心運動定理比較方便;但在研究流體運動時,由於質心的坐標難以確定,用動量定理比較適宜。質點是質點系的一個特殊情況,故動量定浬也適用於一個質點。
參考文獻
1、詞條作者:戴宗信.《中國大百科全書》74卷(第一版)力學 詞條:動量定理:中國大百科全書出版社,1987 :118頁.

