計算公式
零比零型
 洛必達法則
洛必達法則 洛必達法則
洛必達法則若函式 和 滿足下列條件:
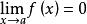 洛必達法則
洛必達法則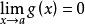 洛必達法則
洛必達法則⑴ , ;
 洛必達法則
洛必達法則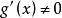 洛必達法則
洛必達法則⑵ 在點 的某去心鄰域內兩者都可導,且 ;
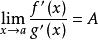 洛必達法則
洛必達法則 洛必達法則
洛必達法則⑶ ( 可為實數,也可為 ±∞ ),則
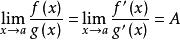 洛必達法則
洛必達法則無窮比無窮型
 洛必達法則
洛必達法則 洛必達法則
洛必達法則若函式 和 滿足下列條件:
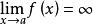 洛必達法則
洛必達法則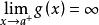 洛必達法則
洛必達法則⑴ , ;
 洛必達法則
洛必達法則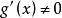 洛必達法則
洛必達法則⑵ 在點 的某去心鄰域內兩者都可導,且 ;
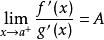 洛必達法則
洛必達法則 洛必達法則
洛必達法則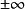 洛必達法則
洛必達法則 洛必達法則
洛必達法則⑶ ( 可為實數,也可為 或 ),則
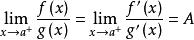 洛必達法則
洛必達法則其他不定式
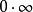 洛必達法則
洛必達法則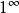 洛必達法則
洛必達法則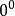 洛必達法則
洛必達法則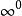 洛必達法則
洛必達法則 洛必達法則
洛必達法則 洛必達法則
洛必達法則 洛必達法則
洛必達法則不定式極限還有 , , , , 等類型。經過簡單變換,它們一般均可化為 型或 型的極限 。
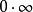 洛必達法則
洛必達法則(1) 型
 洛必達法則
洛必達法則 洛必達法則
洛必達法則可將乘積中的無窮小或無窮大變形到分母上,化為 型或 型 。
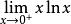 洛必達法則
洛必達法則例:求
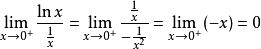 洛必達法則
洛必達法則解:原式=
 洛必達法則
洛必達法則(2) 型
 洛必達法則
洛必達法則把兩個無窮大變形為兩個無窮小的倒數,再通分使其化為 型 。
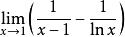 洛必達法則
洛必達法則例:求
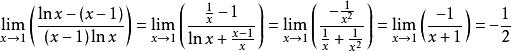 洛必達法則
洛必達法則解:原式=
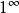 洛必達法則
洛必達法則(3) 型
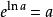 洛必達法則
洛必達法則可利用對數性質 將函式化簡成以e為底數的指數函式,對指數進行求極限 。變化方法如下
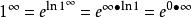 洛必達法則
洛必達法則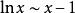 洛必達法則
洛必達法則同時針對不同的問題,還可以利用等價無窮小 作替換,化簡算式。
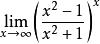 洛必達法則
洛必達法則例:求
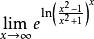 洛必達法則
洛必達法則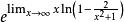 洛必達法則
洛必達法則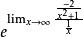 洛必達法則
洛必達法則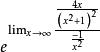 洛必達法則
洛必達法則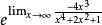 洛必達法則
洛必達法則解:原式= = = = =
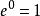 洛必達法則
洛必達法則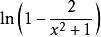 洛必達法則
洛必達法則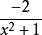 洛必達法則
洛必達法則=,上式求解過程中,利用了等價無窮小的替換,即把 替換成了 。
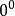 洛必達法則
洛必達法則(4) 型
同上面的化簡方法
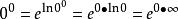 洛必達法則
洛必達法則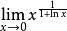 洛必達法則
洛必達法則例:求
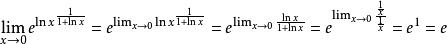 洛必達法則
洛必達法則解:原式=
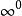 洛必達法則
洛必達法則(5) 型
同上面的化簡方法
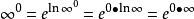 洛必達法則
洛必達法則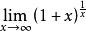 洛必達法則
洛必達法則例:求
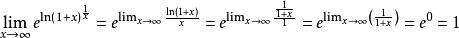 洛必達法則
洛必達法則解:原式=
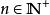 洛必達法則
洛必達法則注意:不能在數列形式下直接用洛必達法則,因為對於離散變數 是無法求導數的。但此時有形式類近的斯托爾茲-切薩羅定理(Stolz-Cesàro theorem)作為替代 。
定理推廣
 圖1 法國數學家-洛必達
圖1 法國數學家-洛必達 洛必達法則
洛必達法則⑴ 該定理所有條件中,對 的情況,結論依然成立 。
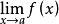 洛必達法則
洛必達法則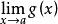 洛必達法則
洛必達法則 洛必達法則
洛必達法則⑵ 該定理第一條件中, 和 的極限皆為 時,結論依然成立 。
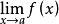 洛必達法則
洛必達法則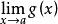 洛必達法則
洛必達法則 洛必達法則
洛必達法則 洛必達法則
洛必達法則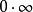 洛必達法則
洛必達法則 洛必達法則
洛必達法則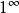 洛必達法則
洛必達法則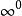 洛必達法則
洛必達法則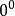 洛必達法則
洛必達法則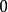 洛必達法則
洛必達法則 洛必達法則
洛必達法則⑶ 上述 和 的構型,可精煉歸納為 、 ;與此同時,下述構型也可用洛必達法則求極限,只需適當變型推導: 、 、 、 、 。(上述構型中 表示無窮小量, 表示無窮大量)
套用條件
在運用洛必達法則之前,首先要完成兩項任務:一是分子分母的極限是否都等於零(或者無窮大);二是分子分母在限定的區域內是否分別可導。如果這兩個條件都滿足,接著求導並判斷求導之後的極限是否存在:如果存在,直接得到答案;如果不存在,則說明此種未定式不可用洛必達法則來解決;如果不確定,即結果仍然為未定式,再在驗證的基礎上繼續使用洛必達法則 。
注意事項
求極限是高等數學中最重要的內容之一,也是高等數學的基礎部分,因此熟練掌握求極限的方法對學好高等數學具有重要的意義。洛比達法則用於求分子分母同趨於零的分式極限 。
 洛必達法則
洛必達法則 洛必達法則
洛必達法則 洛必達法則
洛必達法則 洛必達法則
洛必達法則⑴ 在著手求極限以前,首先要檢查是否滿足 或 型構型,否則濫用洛必達法則會出錯(其實 形式分子並不需要為無窮大,只需分母為無窮大即可)。當不存在時(不包括 情形),就不能用洛必達法則,這時稱洛必達法則不適用,應從另外途徑求極限。比如利用泰勒公式求解 。
⑵ 若條件符合,洛必達法則可連續多次使用,直到求出極限為止 。
⑶ 洛必達法則是求未定式極限的有效工具,但是如果僅用洛必達法則,往往計算會十分繁瑣,因此一定要與其他方法相結合,比如及時將非零極限的乘積因子分離出來以簡化計算、乘積因子用等價量替換等等 。
 洛必達法則
洛必達法則 洛必達法則
洛必達法則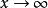 洛必達法則
洛必達法則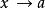 洛必達法則
洛必達法則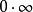 洛必達法則
洛必達法則 洛必達法則
洛必達法則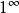 洛必達法則
洛必達法則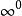 洛必達法則
洛必達法則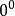 洛必達法則
洛必達法則⑷ 洛必達法則常用於求不定式極限。基本的不定式極限: 型; 型( 或 ),而其他的如 型, 型,以及 型, 型和 型等形式的極限則可以通過相應的變換轉換成上述兩種基本的不定式形式來求解 。

