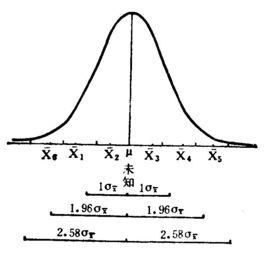
定義
無偏估計
無偏估計 無偏估計 無偏估計 無偏估計 無偏估計設總體ξ的機率分布函式為F(x;θ)，其中x為變元，θ∈Θ為未知參數，Θ稱為參數空間。(ξ，ξ，…，ξ)為取自總體ξ的隨機樣本，若 (ξ…，ξ)是參數θ的一個估計量，且對一列θ∈Θ關係式E( (ξ…，ξ))=θ成立，其中，E[ (ξ，ξ，…，ξ)]表示數學期望，則稱 (ξ…ξ)為θ的無偏估計，並稱 具有無偏性。
例如，估計總體平均值μ時，若以樣本平均值ξ'為估計量，則可算得ξ'的數學期望E(ξ')=μ，這說明ξ'是總體平均值μ的無偏估計。
無偏估計 無偏估計 無偏估計當n→ 時，對一切θ∈Θ，若有 E[ (ξ，ξ，…，ξ)]=θ，則稱 (ξ，ξ，…，ξ)為θ的漸近無偏估計。
具有上述無偏性的估計稱為無偏估計。在統計學中，總體參數的估計基本上都是無偏估計。
有偏估計
無偏估計 無偏估計 無偏估計 無偏估計 無偏估計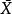 無偏估計
無偏估計若 的數學期望不為θ，即E( )≠θ，包括E( )>θ和E( )<θ，則稱為θ的有偏估計。其中，當E( )>θ時，為偏高估計；當E( )<θ時，為偏低估計。例如，若樣本方差取s=Σ(X- )/n，則E(s)<σ，s與σ的有偏估計(偏低估計)。
優良性
無偏估計的優良性可以從下面兩個方面給予機率論解釋。
沒有系統偏差
無偏估計
無偏估計無偏性的實際意義是指沒有系統性的偏差。統計推斷的誤差有系統誤差和隨機誤差兩種。無論用什麼樣的估計值 去估計 ，總會時而對某些樣本偏高，時而對另一些樣本偏低。而無偏性表示，把這些正負偏差在機率上平均起來，其值為零，即無偏估計量只有隨機誤差而沒有系統誤差。例如，用樣本均值作為總體均值的估計時，雖無法說明一次估計所產生的偏差，但這種偏差隨機地在0的周圍波動，對同一統計問題大量重複使用不會產生系統偏差。
但是需要注意的是，所謂“平均為零”只有在大量重複使用此模型時才能體現出來。關於這一點，需要用大數定律作進一步解釋。
解釋
無偏估計 無偏估計 無偏估計構想進行m次重複抽樣，對 進行估計。第i次的樣本記為X(i)，估計量為 (X(i))。設X(1)，X(2)，…，X(m)是獨立同分布的。若具有無偏性，按照強大數定律，有
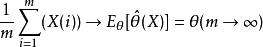無偏估計 無偏估計 無偏估計 無偏估計 無偏估計這即是說，儘管一次估計的結果 (X(i))不一定恰好等於θ，但在大量重複使用時，多次估計的算術平均值可以任意接近待估參數θ的真實值。若估計量 只使用一次，則無偏性這個概念實際上說明不了什麼問題，因為 的無偏性並不能保證在任何情況下，估計 必等於θ。
無偏估計無偏估計量 與θ的偏差的平均值隨使用次數的增多而趨於零。因此，無偏性只有在多次重複使用中，各次誤差相互抵消，才能顯出其優良性。無偏估計並不總是存在的，如服從二項分布的總體B(n，p)，0<p<1，則1/p的無偏估計就不存在。有時，無偏估計雖然存在，但不夠合理。又有些問題中，無偏估計很多，則其優良性由它們的方差來決定，方差越小越優良。
性質
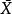無偏估計(1) 樣本均值是總體期望E[X]的無偏估計；
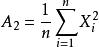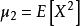無偏估計
無偏估計(2) 樣本二階原點矩是總體二階原點矩的無偏估計；
無偏估計
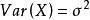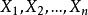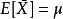無偏估計
無偏估計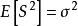
無偏估計
無偏估計(3) 對任意總體 X ，若 E (X)=，，是來自總體X的樣本，則，；
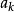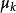無偏估計
無偏估計(4)當總體X的k階矩存在時，樣本的 k 階原點矩是總體 k 階原點矩的無偏估計，但對 k 階中心矩則不一樣。
無偏估計 無偏估計 無偏估計 無偏估計 無偏估計 無偏估計(5)無偏性不具有不變性若是的無偏估計，一般而言，其函式g ()不是g()的無偏估計，除非 g ()是的線性函式。
存在問題
(1)無偏估計有時並不一定存在。
(2)可估參數的無偏估計往往不唯一。統計學中，將存在無偏估計的參數稱為可估參數，可估參數的無偏估計往往不唯一，而且只要不唯一，則即有無窮多個。一個參數往往有不止一個無偏估計。
(3)無偏估計不一定是好估計。
